VIGAS CURVAS EN FLEXIÓN
“La sabiduría es un adorno en la prosperidad y un refugio en la adversidad.”
Aristóteles
4.0.- INTRODUCCIÓN
Entendemos por vigas, en general a aquellos elementos en los cuales una de sus dimensiones es mucho mayor que las otras dos que lo componen.
La viga curva en flexión constituye un importante elemento estructural de ingeniería, debido a su utilización en una amplia variedad de aplicaciones; así por ejemplo estructuras como hélices de helicópteros, ventiladores, turbinas y sub-sistemas de estructuras más complejas pueden ser modelados como vigas curvas De igual manera dichas vigas son usadas de forma corriente en la construcción de puentes. Los ejemplos anteriores permiten afirmar que el estudio de la respuesta dinámica de este componente estructural bajo diversas condiciones, ayudaría a entender el comportamiento de ciertas estructuras reales de mayor complejidad sometidas a condiciones similares.
4.1.- ESFUERZOS EN VIGAS CURVAS EN FLEXIÓN
Para determinar la distribución del esfuerzo en un elemento curvo en flexión se que:
La sección transversal tiene un eje de simetría en un plano a lo largo de la longitud de la viga.
Las secciones transversales planas permanecen planas después de la flexión.
El módulo de elasticidad es igual en tracción que en compresión.
El eje neutro y el eje centroidal de una viga curva, no coinciden y el esfuerzo no varía en forma lineal como en una viga recta.
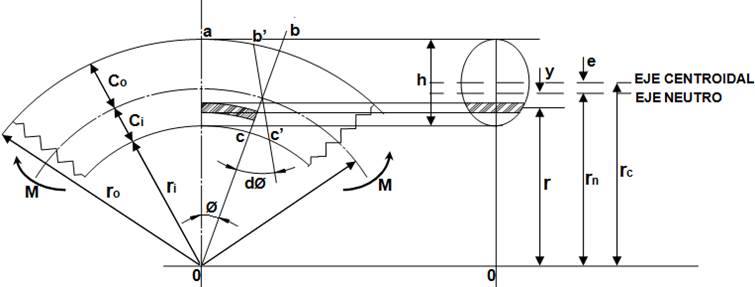
Fig.4.1 Variación lineal de los esfuerzos en una viga recta y su distribución hiperbólica en una viga curva
ro = Radio de la fibra externa.
ri = Radio de la fibra interna.
rn = Radio del eje neutro.
rc = Radio del eje centroidal.
h = Altura de la sección.
co = Distancia del eje neutro a la fibra externa.
ci = Distancia del eje neutro a la fibra interna.
e = Distancia del eje neutro al eje centroidal.
M = Momento flexionante, un M positivo disminuye la curvatura.
El radio del eje neutro viene dado por: 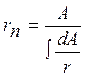 (Ec 4.1)
(Ec 4.1)
Donde: A = Área de la sección transversal
El esfuerzo se determina por: 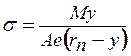 (Ec 4.2)
(Ec 4.2)
La distribución del esfuerzo es hiperbólica y los esfuerzos críticos ocurren en las superficies interna y externa donde: y = ci y y= -co respectivamente, el momento es positivo conforme está representado en la figura.
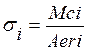 (Ec 4.3)
(Ec 4.3) 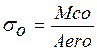 (Ec4.4)
(Ec4.4)
![]() : Esfuerzo de flexión en la fibra interna.
: Esfuerzo de flexión en la fibra interna.
![]() : Esfuerzo de flexión en la fibra interna.
: Esfuerzo de flexión en la fibra interna.
A este esfuerzo se debe añadir el esfuerzo de tracción.
EjemploN°4.1: Grafique la distribución de los esfuerzos que actúan en toda la sección A-A del gancho de grúa de la fig. La sección transversal es rectangular con b=0.75” y h=4” la carga a levantar es de 5000 lb.
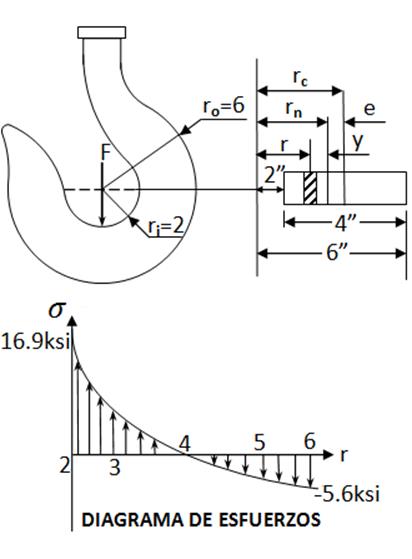
Solución:
Área = A = bh = 0.75 x 4 = 3” pulg2
dA = b.dr
Se sabe que:
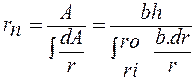
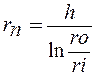
Reemplazando valores:
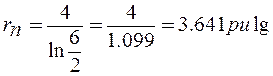
Por tanto la excentricidad:
![]()
El momento M (positivo)
![]()
El esfuerzo será:
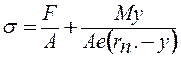
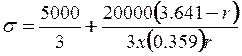
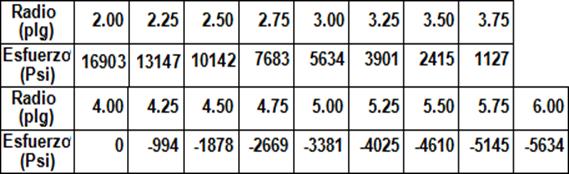
Sustituyendo los valores de r de 2 a 6 se puede elaborar la siguiente tabla:
Tabla 4.1.- Distribución del esfuerzo para 2 < r >6