1 Introduction

The Great Recession was not anticipated by the models. Consequently, some economists, Krugman heading them, have actually asked to shelve all the work conducted in this field for the past 30 years; others think that the time has come for critical reviews and appropriate amendments.

In this work we will use seven univariate models and three multivariate models: VAR-VECM, neural networks and the Kalman filter. According to the critique of Sims [1980], the VAR models were becoming one of the most used tools in econometrics; Granger [1981] and Engle & Granger [1987] laid the foundations of the concepts of integration and cointegration. Johansen & Juselius [1982] introduced a test to find the cointegration range. Boswijk & Doornik [2003] provided an overview of the current status of the estimated VAR-VECM models with constraints and their implementation in a variety of available software packages. The first work on neural networks dates back to 1943, and their application to economics began to spread from the 1980s; nowadays, while for some they are only a passing fad, for others they are the main focus of their research. Kalman published his article in 1960. Until the 1980s only sporadic economic applications were carried out, while in engineering fields their application was spectacular. Since the mid-1980s their application in economics has been gradual and continuous.

Diebold [1997] provided a good summary of the history of macroeconomic ideas versus models and introduced a classification of structural and non-structural models. An overview of the predictive ability of VAR models and their variations was given by Clark et al. [2012]. Given the current situation of disbelief regarding economic models, Wieland et al. [20102] proposed an open database on the Web to compare models and increase the degree of confidence in them. Don [2001], from his privileged position, made a general recommendation on how to proceed with model elaboration and the problematic between the practitioner and the user of the economic models. A review of the different sources of errors and other problems relating to them and their solution was performed by Stekler [2007].

This paper applies twenty different kinds of models to estimate their appropriateness when making predictions in the short term. The work is part of a more specific line of study consisting of R&D as a driver of economic growth.

We apply different mathematical apparatuses to annual macroeconomic time series in order to estimate their ability to fit the observation and predict the short term for 14 countries and 14 series per country; we try to determine whether their fitting and prediction capabilities are influenced on one hand by the type of economic series and on the other by the case of stationariness of the series. The models that we use for single-variable models are “Naïve,” exponential smoothing, Arima, trend, the Kalman filter with only level components and the Kalman filter with both level and trend components. For multivariable models we use VECM models, neural networks and the Kalman filter.

The work provides a new approach to the problem of choosing the cointegration range in VECM models when the number of samples is limited and there are some I(2) series without the necessity of passing to the grade 2 VECM paradigm. In addition, this paper is novel in the number of predictions made ​​in order to reinforce the results obtained: there are 20 models for 14 countries and for each case model–country 12 predictions are made.

Section 2 deals with the input data and section 3 explains how to classify series according to their stationariness. Section 4 differentiates between predictions and adjustments and how they are measured in this paper. Section 5 is devoted to seven univariate models, sections 6 to 8 deal with the multivariate models already mentioned and section 9 is dedicated to the results and discussion, finishing with the conclusions.

2 Input data 1

The fourteen selected countries are the G7, the three Nordic countries, Switzerland, the Netherlands, Belgium and Austria. Their acronyms, in accordance with the OECD (from which the raw input data were obtained) are: USA, CAN, DEU, FRA, ITA, JPN, GBT, AUT, BEL, NLD, DNK, CHE, NOR and SWE. Their choice is conditioned by having a perfectly liquid currency and a floating exchange rate regime during the sample period. In this way, with these 14 currencies, it is possible to build another common reference currency, referred to in this paper as G14. This is such that the sum of the relative increases of 14 coins in each period is zero. Some of the series are denominated in this new reference G14 and others in their national currency (UN). The numeraire G14 is built is such a way that the total relative increments in each period are zero; the same is applicable to series PPM and RE.

The periodicity of the data is annual and ranges from 1970 to 2011 with 42 samples per series. The series are based on the constant 2005 currency and series 5 through 11 are referenced to units per person of working age. Some series are in the local currency and others in the reference currency, G14. The series are:

• ER: exchange rate to the currency of reference in UN/G14.
• PPM: ratio of prices of that country to the weighted common reference inflations of 14 countries.
• RE: real effective exchange rate. RE = 1/ER/PPM.
• LIR: long-term interest rate.
• iM: increase in each period of the monetary aggregate M1.
• EXIM: accumulation of exports over imports; this is the accumulated sum of the trade balance of the previous years in the sample. It is in the G14 reference currency.
• EXIMd: exports minus imports of each period in the G14 currency.
• EXP: exports in the G14 currency.
• IMP: imports in the G14 currency.
• GDPA: the autonomous spending of GDP, i.e. GDP = GDPA1 + EXP - IMP; this is in the local currency.
• GDP: in the domestic currency.
• Erdo: the exchange rate to the dollar in UN/$.
• lER: the natural logarithm of ER.
• iRE: the increase of ER in each period.

The last two series are included to assess whether the adjustment capability (AC) and prediction capability (PC) are influenced by the scale used.

3 Stationary series

We use the ADF test (augmented Dickey–Fuller) to classify the input series into six classes depending on whether the series is stationary or not and whether in turn it has trend and drift components. The test performs the following regression, where k is the number of lags to compensate for residual autocorrelation; k is optimized for a maximum value of 4 to minimize this effect.

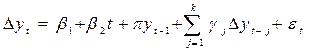,                                                            (1)
where Dy is the increment of the variable, β1, b2, pand g are parameters and εt is a zero-mean Gaussian process.

The cases as a function of the three parameters are as follows:

• Case 1: stationary with zero mean (π ≠ 0, β1 = 0, β2 = 0)
• Case 2: stationary with non-zero mean (π ≠ 0, β1 ≠ 0, β2 = 0)
• Case 3: stationary linear trend (π ≠ 0, β1 ≠ 0, β2 ≠ 0)
• Case 4: not stationary without drift (π = 0, β1 = 0, β2 = 0)
• Case 5: not stationary with drift (π = 0, β1 ≠ 0, β2 = 0)
• Case 6: not stationary with drift and trend (π = 0, β1 ≠ 0, β2 ≠ 0)

The frequencies for all the cases are as follows:

Case	1	2	3	4	5	6	Total
Total	33	2	106	3	2	50	196

4 Adjustment and prediction

Both the AC and the PC will be measured with two criteria. The first criterion will be applied by grouping the series by the kind of economic series, i.e. ER, EXP2, etc. The second criterion in turn will be applied by grouping the series by the degree of stationariness that the ADF test has given.

  The first criterion for the AC is the ratio between the estimated and the total sum of squares, such that R2 = ESS/TSS, the estimated versus the total sum squared. Each series has its R2 calculated on the total number of samples n; the first line of each group in Table 1 is the average value of this figure for 14 countries, which is a value between [0,1] that indicates the degree of fitting between the original series and the one modeled within the sample period. The second criterion is the number of times that the estimated series adjusts better, equal to or worse than the baseline model (Naïve model). Lines 1–3 of Table 2 indicate these results, and line 4 in Table 2 shows the non-applicable cases.

The first criterion for the PC is calculated as the RSS (standard error) weighted by the average value. Lines 2–4 of each group in Table 1 depict these values for 1-, 2- and 3-year forecasts. For each series we make 4 forecasts for the last 4 samples and we calculate the average for the 14 countries: a mean of 56 values. The second criterion is the same as for the AC; lines 3–6 of Table 2 indicate how many of all the series make predictions that are better than, equal to or worse than the reference method.

5 Univariate models

The first method to consider is the “Naïve” one, which consists of taking as the predicted value the one observed earlier; what this means is that the series is a pure random walk (PRW). Therefore, we have:

.
                                                                                                                                 (2)
As the simplest of all the models, this becomes the reference one and we will compare the performances of the others with this baseline model. 

The exponential smoothing method, “ExpSmo” in the tables, decomposes the signal into the structural components that best fit the end result, being trend, cycle and residual components. The trend component could be two additive, two multiplicative or none; on the other hand, the cycle components could be none, additive or multiplicative, making in total 15 possible exponential smoothing models. Fortunately, tools exist that automatically make the best choice and calculate the model for us.

The Arima(p,d,q) method depends on three parameters; the second, d, is the number of times that the series has to be differentiated to become stationary in such a way that we may apply an Arma(p,q) model to the residuals:

.     (3)

For each series, we find the values ​​of d, p and q that minimize the standard error in the sample.

The fourth model to analyze is the components model, “Comp” in the tables. This method consists of making the trend of the series a polynomial of sufficient degree that the residuals become a stationary series. We apply an Arma(p,q) model to the residuals. For the trend component the polynomial is extrapolated and a prediction of the residuals is made; both figures are added to complete the forecast.

The trend model, “Trend” in the result table, consists of prolonging the tendency of the series.

The sixth and seventh models are Kalman filters; the first is called the level model and the second the level and trend model. The first involves one state and the second two states. They are given in the table as “Kalman1A” and “Kalman2A.”

For Models 2 to 4 and for the ER, PPM and RE series we proceed to evaluate the predictions according to their models, but in every prediction step we correct the relative increases in such a way that the sum of all the percentage changes for the 14 countries must equal zero. This is possible due to the way in which we have defined these three series. Thus, in every step in which we evaluate the prediction for each country, we obtain the sum of the percentage increases for the 14 countries and the forecast for every country is corrected according to the weight of each country in the reference currency G14. The reference currency G14 is designed in order to determine whether this procedure can improve the predictions. Table 3 shows the names and results of these four models beside the reference baseline model, the “Naïve” model.

6 Multivariate models: VECM

The paradigm of the linear regression was widely used for regressions containing both stationary and non-stationary series until the critique of Sims [1980]. If the VAR (vector autoregressive) models are the extension of the linear regression for several equations’ regressions when all the series are stationary, the VECMs (vector error correction models) are for the case in which at least one of the series is not I(0) but none is I(2). The VAR model for a vector y of p variables is defined as:

                                                            (4)

where A are matrices pxp, εt is a p error vector such that N (0, σ) and k is the number of lags.

This model can also be written in the following two ways:

,                          (5)

which is the VECM of the long term, and the next is the short-term one; this short-term formulation is the one that we use herein:

.           (6)

where:
                                                    (7)
                                                                        (8)

P=abT being the long-term impact matrix, the Γ matrices measure the short-term impact of transient effects. There are deterministic relationships between the matrices A, G  and G*. In the case of a cointegration matrix, P is of reduced rank and its dimensions are kxr, r being the cointegration range.

We will build models of 6 and 8 series but these models will be a mixture of series I(0), I(1) and I(2); although, strictly speaking, when any of the series are I(2) we cannot apply this model, we will see that in the case that they are not excessive and the number of unit roots is under some control, we can still apply this powerful VECM paradigm. This is the situation that we find most commonly in applied research. We impose two conditions: on one hand, the number of roots larger than 1 is small, and on the other hand, the residual marginally passes five diagnostic tests; we call these models marginally stable models. To them we apply the procedures and conclusions of the strict VECM models, strict meaning that that all the series are I(0) or I(1) and any is I(2).

6.1 Choice of k, number of lags and r and the cointegration range

We use the Johansen test, which gives the values ​​of r that minimize the maximum likelihood function for the two criteria “eigen” and “trace.” We face several simultaneous problems here: one is the small number of samples; another is the existence of series that are not strictly I(1), but marginally I(2); the third is the power of the test itself; and the fourth is the discrepancy of values ​​provided by the test along the two criteria. To circumvent all these obstacles, we compute and compare the following topics for two values ​​of k (2 and 3) and for all possible values ​​of r, which will help us to make the best choice for k and r:

• The Johansen test result for r is case K = 2, 3 according to the two criteria “eigen” and “trace.”
• The number of unit roots of the accompanying form.
• The results of five diagnostic tests for residuals for all the cases: k = 2, 3 and r = 1 to rmax. The five tests for residuals are: normality, kurtosis, skewness, heteroskedasticity and residual autocorrelation.

For each of the models generated we will discuss the selection of k and r, taking into account the above descriptions.

6.2 VECM models of six variables

We take the following six series for our model number 8 (#8, see Table 1 header), called “Vecm6ASi” in the tables: ER, PPM, RE, LIR, iM and EXIM. In principle, the intention is to ascertain whether there is any relationship between the series that would make the monetary variables of an open economy. Therefore, we have 14 models, 1 per country, to adjust and predict 84 series. We obtain a value of 2 for k in 12 cases and a value of 3 in 2 cases; r in turn takes a value in the range 1 to 5 for the 14 cases. With this choice, all the countries pass the 5 diagnostic tests except JPN, which fails the test of normality of the residuals.

In Model #8 we change the series “EXIM” for “EXIMd” for possible improvements in the results since there are 18 I(2) series of a total of 84 in Model #8 and this figure is reduced to 8 in Model #9. This Model #9 is marked in the tables as “Vecm6BSi.” Regarding the choice of k now, it is 3 only in 1 case and r takes a value between 1 and 3. Reviewing the diagnostic tests, we found problems only in the case of JPN, but now we find problems with 5 diagnostic tests instead of 1, which is somewhat unexpected.

To these two models (#8 and #9) and for the three first series, we apply the constraint of zero sum of the relative increments. In this way, we generate two additional models (#10 and #11), marked in the tables as “Vecm6ACo” and “Vecm6BCo.” We expect an improvement of the prediction capability of these models with regard to the two previous ones.

6.3 VECM models of eight variables

We proceed to build three new models, in this case with 8 variables per model. We keep fixed the choice of series and we change the values ​​of k and r as follows: Model #11 (“Vecm823”) sets k = 2 and r = 2, Model #12 (“Vecm8opti”) optimizes the two parameters as explained in the previous paragraph, resulting in values ​​of k = 2 for all cases and r varying from 3 to 7; the third model in this class is #13 (“Vecm827”), which fixes k = 2 and r = 7. Thus, we want to see what happens with the fitting and predicting capabilities based on the cointegration range chosen. The selected series are ER, PPM, RE, LIR, iM, EXP, IMP and GDPA, which are a mix of monetary and fiscal series for different countries.

7 Neural networks

We can consider in our case a neural network (“NeuNet” in the tables) as a black box that accepts “pi” input variables, giving “ps” output variables, and inside the box it is possible to specify the number of nodes m, the internal relations laws, the maximum error that we accept in the output variables, which we call “err1,” and the minimum value of the partial derivatives of error functions, which we call “thres1.” For the 14 countries and for the first 11 series, we create a network (model) taking as the input the 8 series selected in the previous section (these will be the explanatory series) and 3 outputs: predictions for 1, 2 and 3 years ahead of the one single-output series. First, we find the minimum values of m that make the network converge for the given “err1” and “thres1” and fix a maximum value of m equal to 200. We obtain this convergence training the network for values ​​of m between 10 and 200 except in 17 of the 154 cases. With these 3 parameters, we obtain the predictions, calculating the network, and the adjusted values.

8 Kalman filter for several variables

A Kalman filter, or state space model, for p observations yt and m states αt, where t is time 1 .... n, is defined as:

                                                                                          (9)
                                                                                    (10)

where:

,                                        

are independently and equally distributed Gaussian stochastic processes. For general models we can relax the condition of normality, though we will keep it here.

The dimensions are:

• y: vector of observations px1
• Z: transformation matrix from states to observation, pxm
• H: pxp, covariance of errors in the observation equation
• Q: sxs, matrix of covariance error in the state equation
• R: mxs, reduction matrix in the state equation
• a1: mx1, initial value of the average of the states
• P1: mxm, initial value of covariance of the states

In turn, the matrices Z, M, T, R and Q may be time-dependent.

The simplest model is called a level model, where p = 1, m = 1 and the matrices Z, H, T, R and Q have a 1 x 1 dimension. The next model is the level and trend model, where p = 1, m = 2, H and R are scalar, T and Q are 2 x 2 and Z is 1 x 2. These two models are those applied above in the paragraph on univariate models.

Here we consider models that have five observations: one is the explained variable and the other four the explanatory variables; the four coefficients of these explanatory variables are the states. This is a Kalman filter based on a regression without intercept for four regressors and one regressand. The dimensions in this case are: p = 1, m = 4, n = 42, dim (Z) = 1 x 4 x 42, dim (H) = 4 x 4, dim (Q) =4 x 4, dim (R) = 4 x 4, dim (a1 ) = 4 x 1 and dim (P1) = 4 x 4.

For each country and for the first eleven series we build a model that will estimate this series against four other series (regressor or explanatory) as follows (the explanatory series are chosen according to the relationship with the explained series):

                                    (11)
                                          
                                                   
                                                    
                                                          
                                                 
                                             
                                                     
                                                     

                                                                                                                                         
Some of these equations are reminiscent of the classic IS-LM model of the open economy. The question here is whether we can interpret the value and variation of the coefficients as explanatory laws that underlie the relationship between the variables and the response; in our view, such an exercise is not pertinent.
                                                                                                                                         
9 Results

Table 1 presents the results according to the first criterion for AC and PC. The rows are for 14 groups, 1 for each type of economic series, and the columns are for the different models. For each group the first line is the adjustability and the other 3 lines the forecast capability at 1, 2 and 3 years ahead. Table 2 presents the results according to the second criterion; the first 4 lines are the AC and the following 4 lines the PC for 1-, 2- and 3-year forecasts and non-applicable cases, respectively. In each group the first line is the number of cases in which the capability is better than the PRW, line 2 is the case in which it is equal and line 3 is the case in which it is worse. Table 2 was designed to show whether there is any correlation between these capabilities and the case of stationariness of the series (remember that we have classified the whole set of series into 6 cases); this information is not shown for reasons of space and because we have not found any correlation. In other words, there is no relationship between the AC and the PC and the different cases of stationariness.

Table 3 has the same structure as Table 1 and is devoted to the case of three series for which the constraint is applied to the sum of the relative changes in each step of prediction. It has already been mentioned that this procedure does not make ​​any improvement in either capacity.

Two other series changing the scale of the ER series are included: one uses the natural logarithm and the other the increment. The first option leaves, as expected, the two capabilities unchanged and the second is seriously degraded.

The cases in which significant improvement is achieved are shaded in the tables; in addition, when degradation is observed, it is signaled by hard-shadowing.

9.1 Results for the univariate models

The ability to adjust for the exponential smoothing models with the first criterion is very close to that of the baseline model without exceeding it. The AC is degraded in two cases. According to the second criterion, this capability remains the same. The predictive capability approaches the baseline model but is only exceeded in three of fourteen cases; according to the second criterion, this model has the same capacity as the baseline model.

The result for the Arima model is as follows: for all but two cases, according to the first criterion, the model neither predicts nor adjusts better than the baseline model; the two cases in which it performs better are the series EXIMd and iM1. The preliminary conclusion is that this model behaves better for series in differences and with increment scales than for series with absolute scales. Taking all the series according to the second criterion, this model slightly worsens the two capacities versus the baseline.

For the results of the component models, we can repeat exactly the results for the ARIMA case except that according to the second criterion the prediction ability is still worse than that of the Arima case. For the trend model, in any case, it fits better than the baseline model and only in four cases it improves the prediction capability with the first criterion. For the second criterion, we could say that this is a model with capabilities that are very similar to the reference.

Interestingly, the first Kalman model clearly improves the fitting capability and in many cases it reaches the maximum value of unity. The second method does not surpass the fitting capability of the baseline model. Regarding the predictive power and the first criterion, the first model never exceeds the baseline model and the second is better in four cases. Using the second criterion, the level model has an AC equal to the baseline and the level and slope model has a worse PC than the baseline model.

Table 3 shows the results for the four models with restrictions in the relative increments of the first three series: they do not improve in any of the four cases for these univariate models; we can see that for some of the multivariable models this procedure significantly improves the prediction capability.

9.2 Results for the multivariate VECM models

Using the first criterion for the first VECM model of six variables, we can see that the AC of this model slightly improves the baseline in two cases and is degraded in one case with respect to PRW. If we use the second criterion, this capacity remains the same. The ability to predict improvements is shown in two of the six cases using the first criterion and according to the second criterion this capability would be worse than the PRW.

In Model #9, compared with the previous models, we see that the adjustability improves slightly, outperforming the baseline model, but the forecasting performances are worse than those of Model #8.

For Models #10 and #11, it was hoped that a substantial improvement in the fitting and predictive ability would be achieved with respect to the previous two models, but the reality is that this does not happen. The results are shown in Tables 1 and 2.

For the three VECM models with eight variables, we can state that the ability to adjust residually improves versus the PRW; the PC is better than the PRW in only one case. This is according to the first criterion; for these three models, a harder conclusion is derived according to the second criterion: the optimal choice of cointegration range has no influence, the adjustment capacity remains virtually unchanged and the PC is significantly worse than the PRW for all these three models.

The VECM models are over-parameterized ones. Once the values ​​of p, k and r have been found, as explained above, the next step is to reach a just-defined model imposing a restriction on matrices α and β. In a just-defined model we can derive the laws and rules that govern, in the long and short term, the relationships between the variables. In the literature there are many examples (Johansen, Juselius, Pfaf, etc.) of proceeding in this way but they are always for very low values of p. Another limitation is the tool used in our case, which allows us to analyze a limited number of possibilities on the imposed restrictions. However, before delving into the possible relationships between the variables, we would have to find for which set of series ​​and in which time window we are able to make a model that at least approaches the PRW capabilities. Without the necessity of having a just-defined model, we can process and compute the equivalent VAR and apply an impulse response analysis and a forward variance decomposition analysis, being one of the forms of robustness of the VAR paradigm. An alternative is to construct a SVECM (structural VECM) and apply yet more restrictions. The ability of these models in the analysis of causality between different variables is remarkable.

In these models, as in almost all models, a key issue is choosing the variables set, periodicity and temporal scope in which we apply the model. The choice of the series is made as close as possible to the medium-term IS-LM models. Regarding the periodicity, it might be more advisable to have chosen at least quarterly periodicity, but the problem is the availability and in turn the question of whether this greater periodicity would improve the demonstrative capacity of this exercise.

9.3 Results for the neural network models

Studying the results, we see that neural networks are far from improving the ability to adjust or predict of the reference model and they place themselves in last position compared with the other models. The result table does not reflect for comparison purposes either the theoretical complexity of the models or the machine time required to solve them; it still gives the possibility for these models to appear in the results tables.

The references are innumerable but for these and the Kalman models we are lacking a paper ​​that makes a quick and concise comparison of the software packages available and their advantages and disadvantages.

9.4 Results of the multivariate Kalman filter models

The table of results, with the first criterion, shows how the adjustment capacity reaches the maximum value in all cases for these models; this is not a surprise as these are strong parameterized models. As for the forecasting capability, in 6 of the 11 cases this capability improved, in 3 cases it remained almost the same and in 2 cases (for the ER and PPM series) it worsened. This point is still to be understood. Considering the second criterion, it is observed that the AC is much better than the PRW, but the predictive power remains virtually unchanged.

9.5 Discussion

The choice of the annual periodicity was motivated by practical reasons; at first glance, it would seem more reasonable to have chosen the quarterly periodicity (for many models the small number of samples is a problem), but otherwise it is not clear that in order to find the internal laws and future projections of economic series, up-sampling would have helped to demonstrate these adjustment and prediction capabilities. The macroeconomic relations in the long run, apart from the Solow model and its derivatives, are very slim. A way forward would be to increase the sample frequency and try to find relationships that fit in the medium term by applying a temporal moving window.

The choice of a common reference currency did not contribute, as was expected, to improving the models’ performances. However, we remain convinced that this is the path to follow in future works. Today, and globally speaking, there are two medium-term fundamentals accumulating disequilibrium in our economies: debtor–creditor positions and the accelerating money creation rate. We propose a model of n + m countries, n being the 14 countries of this paper and m groups of countries that complete a global economy. In this model, beside the common currency, other common references are possible and the contour conditions would make more sense. This is our forward-looking investigation proposal. 

Regarding the uncountable types of models that were not covered in this work, together with variations of those already treated, we can state something about four of them. Differential equations are the normal way to treat any problem when unsure about the rules and laws before building a model; we tried this logic but the preliminary result forced us to abandon this approach. The second is the algorithm, which is scarcely used but promising if you do not believe in general equilibrium. The third are Kalman multivariable models with time-dependent matrices. The fourth are the DSGE models, now occupying a central, prominent and dominant position in economic modeling, but they are beyond the scope of this work.

From the review of the economic model literature, the amount of forecasting everywhere, the effort to generate new models and the scant attention paid to their validation and accuracy are amazing. This defect, that an explosion of models and predictions requires increased effort concerning the validation and the predictive capabilities of the models, is also found in fields of engineering. In the strictly academic sphere the work and effort undertaken to generate and explain the different mathematical models and appliances that are able to fit into the sample period are huge, but comments on their actual predictive capabilities and their validation are limited. The results of the study indicate the difficulty of generating predictive capable models. On the one hand, the paper intends to draw attention to the need to pay less attention to short-term economic forecasting and work around the imbalances and disequilibrium that accrue in the medium term and how to module the future.

Conclusions

A review was carried out of different models applied to macroeconomic time series, highlighting their theoretical simplicity, their ability to fit into the observation period and their forecast capability for one, two and three years ahead. These capabilities were analyzed depending on the type of economic series and on the degree of stationariness of the series.

The models presented, except the multivariate Kalman filter, improve neither the adjustment nor the predictive capacities of the pure random walk model. In many cases the forecast capability worsens. The best fit performances of the Kalman filter merely reflect an over-parameterized model; the question arises when we try to infer the rules and laws that govern the relationship of the series. Changing the parameters within the sample period is a powerful approach to fit inside, but that does not mean that the forecast will improve.

The dispersion of the predictive quality of the different models highlights the pending effort that is needed in the validation and intercomparison of economic time-series models.

References

1	Andersen TG, Davis RA, Kreiβ JP, (2009) “Handbook of Financial Time Series,” Heidelberg, Springer
2	Boswilk HP, Doornik JA, (2003) “Identifying, Estimating and Testing Restricted Cointegrated Systems: An Overview,” Universiteit van Amsterdam
3	Carrasco-Gutierrez CE, et al ., (2007) “Selection of Optimal Lag Length in Cointegration VAR Models with Weak Form of Common Cyclical Features,” Banco Central do Brasil
4	Chui CK, Chen G, (2009) “Kalman Filtering,” 4th Ed, Heidelberg, Springer
5	Clark TE, Ravazzolo F, (2012) “The Macroeconomic Forecasting Performance of Autoregressive Models with Alternative Specifications of Time-Varying Volatility,” Norger Bank, WP 2012/09
6	Copeland L, (2005) “Exchange Rates and International Finance,” Prentice Hall
7	Cowpertwait P, Metcalfe A, (2009) “Introductory Time Series with R,” Heidelberg, Springer
8	Cryer JD, Cahn KS, (2008) “Time Series Analysis With Applications in R,” Heidelberg, Springer
9	Davidson J, (1998) “Structural Relations, Cointegration and Identification: Some Simple Results and their Application,” Journal of Econometric
10	Diamandis PF, Georgoutsos DA, Kouretas GP, (2001) “The Monetary Approach in the Presence of I(2) Components: A Cointegration Analysis of the Official and Black Market for Foreign Currency in Latin America,” Athens University
11	Diebold FX, (1997) “The Past, and Future of Macroeconomic Forecasting,” University of Pennsylvania. www.ssc.upenn.edu/~diebold/
12	Dolado JJ, Gonzalo J, Marmo F, (1999) “Cointegracion,” Universidad Carlos III de Madrid
13	Don FJH, (2001) “Forecasting in Macroeconomics: A Practitioner’s View,” De Economist 149 no. 2
14	Gales M, (2001) “Neuronal Networks,” different handouts, University of Cambridge
15	Greenslade JV, Hall SH, Hendry SG, (1999) “On the Identification of Cointegrated Systems in Small Samples: Practical Procedures with an Application to UK Wages and Prices,” London Business School
16	Gunthet F, Fritsch S, (2010) “neuralnet: Training of Neural Networks,” The R Journal
17	Harris R, Sollis R, (2003) “Applied Time Series Modelling and Forecasting,” Wiley
18	Hendry D F, (1995) “Dynamic Econometrics,” Oxford University Press
19	Hendry DF, Juselius K, (1999) “Explaining Cointegration Analysis,” UK Economic and Social Research Council
20	Johanse S, (1995) “Likelihood-Based Inference in Cointegrated Vector Autoregressive Models,” Oxford University Press
21	Johansen S, Juselius K, (1990) “Maximum Likelihood Estimation and Inference on Cointegration – With Applications to the Demand for Money,” Oxford Bulletin of Economic and Statistic
22	Juselius K, (2006) “The Cointegrated VAR Model: Methodology and Applications (Advanced Texts in Econometrics),” Oxford University Press
23	Lütkepohl H, (2005) “New Introduction to Multiple Time Series Analysis,” Springer
24	Matheson T, Stavrev E, (2013) “The Great Recession and the Inflation Puzzle,” IMF Working Paper, WP/13/124
25	McLeod I ,Yu H, Mahdi E, (2008) “Time Series Analysis with R,” Elsevier
26	Pfaff B, (2008) “VAR, SVAR and SVEC Models: Implementation Within R Package vars,” Journal of Statistical Software
27	Riedmiller M, (2005) “Neural Fitted Q Iteration – First Experiences with a Data Efficient Neural Reinforcement Learning Method,” Heidelberg, Springer
28	Sarno L,Taylor M, (2002) “The Economics of Exchange Rates,” Cambridge University Press
29	Shelter B, Winterhalder M, Timme J, (2006) “Handbook of Time Series Analysis,” Wiley
30	Shumway RH, Stoffer DS, (2011) “Time Series Analysis and Its Applications: With R Examples,” 3rd Ed, New York, Springer
31	Stekler HO, (2007) “The Future of Macroeconomic Forecasting: Understanding the Forecasting Process,” www.econpapers.repec.org
32	Verbeek M, (2008) “A Guide to Modern Econometrics,” Wiley
33	Welch G, Bishop G, (2004) “An Introduction to the Kalman Filter,” University of North Carolina
34	Widi M, (2013) “An Introduction to State Space Models,” Zurich University of Applied Sciences
35	Wieland W, Cwik T, Müller GJ, (2012) “A New Comparative Approach to Macroeconomic Modeling and Policy Analysis,” www.macromodelbase.com/system/files
36	Winker P, Maringer D, (2004) “Optimal Lag Structure Selection in VEC-Models,” University of Erfurt