
EL CAPITAL HUMANO EN LAS TEORÍAS DEL CRECIMIENTO ECONÓMICO
André Gérald Destinobles
Esta página muestra parte del texto pero sin formato.
Puede bajarse el libro completo en PDF comprimido ZIP
(67 páginas, 347 kb) pulsando aquí
EL MODELO DE MANKIW, ROMER Y WEIL (1992)
En el marco del programa de investigación neoclásico[1], el modelo ampliado de Solow, o Modelo de N. Gregory Mankiw, David Romer y David N. Weil (1992) (conocido generalmente como modelo MRW) constituye uno de los modelos de crecimiento empíricos más notable hoy en día para explicar analíticamente los hechos estilizados del crecimiento de una economía y de convergencia. Independientemente de que estemos a favor o en contra, este modelo constituye la piedra angular del resurgimiento del modelo neoclásico en los 90 –tras los numerosos cuestionamientos al que fue sometido por aquellos que buscaban o siguen buscando a partir de sus modelos construidos y/o sus nuevos sondeos teóricos, una explicación endógena del crecimiento efectivo- como marco de referencia en los estudios sobre crecimiento económico y convergencia económica. Por ello, es importante entender sus características, sus predicciones y sus propiedades y revisar ciertas aprobaciones y críticas a las cuales ha sido objeto.
I ) Estructura de base del Modelo de Mankiw, Romer y Weil (MRW) (1992)
El modelo desarrollado por Mankiw y alii (1992) considera una economía cerrada que tiene un solo sector de producción, utiliza el capital físico, el trabajo y el capital humano como principales factores de producción. Cabe señalar aquí, que ese capital humano es asimilable a capacidades, competencias y conocimientos de los trabajadores individuales. Bajo esa óptica, se considera al capital humano como un bien exclusivo y competitivo.
Además, cabe recalcar que este modelo de Mankiw y alii (1992) es una ampliación del modelo Solow-Swan (1956), por lo tanto, hace suya también la hipótesis de rendimientos constantes a escala, hace uso también de la función de producción Cobb-Douglas; después de la contrastación del modelo de Solow-Swan realizado por ellos en torno a qué variables y en qué sentido influirían en el crecimiento y del sesgo al alza observado en las estimaciones, recomendaron incluir la variable capital humano para mejorar la calidad de los resultados del modelo Solow-Swan (1956).
De tal manera que el modelo Mankiw y alii (1992) considera:
I. la siguiente función de producción
, ,
Donde:
® es la producción, es decir, el PIB.
® representa al stock de capital físico y es acumulable a través de la
II. Inversión en bienes de capital: ,
es la fracción de la producción asignada al capital físico
® representa al stock de capital humano, y es acumulable a través de la
III. Inversión en educación: ,
es la fracción de la producción asignada al capital humano
Grosso modo, el ahorro se divide en formación de capital humano y formación de capital físico, y las:
IV. Depreciación del capital físico: ,
V. Depreciación del capital humano: ,
® son, respectivamente, las tasas de depreciación del capital físico y del capital humano.
VI. Ecuación de acumulación del capital físico[2]:
VII. Ecuación de acumulación del capital humano:
Al igual que en el modelo de Solow-Swan (1956), el progreso técnico y el trabajo crecen, respectivamente, a las tasas constantes y exógenas , es decir,
![]() ® es un índice de productividad total de los factores,
resume el estado actual del conocimiento teórico o también llamado progreso
técnico.
® es un índice de productividad total de los factores,
resume el estado actual del conocimiento teórico o también llamado progreso
técnico.
Su tasa de crecimiento es una constante exógena:
VIII. ó
® Es la fuerza laboral o el trabajo.
Su tasa de crecimiento es una constante exógena:
IX. ó
La función de producción es COBB-DOUGLAS, el modelo Mankiw y alii (1992) supone rendimientos constantes a escala.
X. Define: ® Como producto por unidad de trabajo eficiente
XI. Define: ® Como capital físico por unidad de trabajo eficiente
XII. Define: ® Como capital humano por unidad de trabajo eficiente.
SOLUCIÓN DEL MODELO
La función de producción:
puede escribirse
(1)
El producto por unidad de trabajo eficiente es:
(2)
La tasa de crecimiento del stock de capital físico es: (3)
La tasa de crecimiento del stock de capital humano es: (4)
La tasa de crecimiento del stock de capital físico por unidad de trabajo eficiente es:
(5)
La tasa de crecimiento del stock de capital humano por unidad de trabajo eficiente es:
(6)
Las ecuaciones (5) y (6) forman un sistema de ecuaciones diferenciales de primer orden en k y h.
Ahora bien, en el estado estacionario tanto como son iguales a cero.
(5.1)
(6.1)
Igualando (5.1) y (6.1), tenemos: (6.2)
Ahora, sustituyendo (6.2) en (5.1), obtenemos: (7)[3]
que es el valor de k en el estado estacionario, es decir, la economía converge hacia , que define un equilibrio estable.
(6.2) se puede escribir así:
reemplazando esta última ecuación en (6.1), tenemos:
(8)
que es el valor de h en el estado estacionario.
La representación gráfica del sistema formado por las ecuaciones (5) y (6) ó (7) y (8) se puede visualizar a partir del siguiente diagrama de fases.
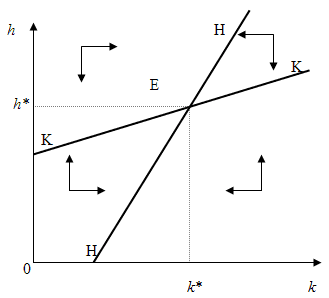
En efecto, a la izquierda (derecha) de la curva KK, es negativo (positivo). Un
análisis similar para el capital humano nos revela que por debajo (por encima)
de la curva HH, es negativo (positivo).
Ahora, reemplazando (7) y (8) en (2), tenemos:
Entonces, el producto por unidad de trabajo eficiente en el estado estacionario es:
(9)
Ahora, tomando el logaritmo de la ecuación 9, tenemos:
Suponiendo que la tasa de depreciación es igual para ambos tipos de capital:
(10)
Esa misma expresión obtenida en el modelo Solow-Swan (1956) con es:
Ahora bien, dado que el producto por unidad de trabajo eficiente no es observable, conviene reescribir la ecuación (10), únicamente en términos de producto por trabajador:
considerando que \
(10’)
Esta expresión, nos indica que en el sendero de crecimiento equilibrado, el nivel de la productividad:
1) está en función de .
2) depende negativamente de las tasas de crecimiento de la población, del progreso técnico y de la depreciación (tasas expresadas en el siguiente término: )
3) depende positivamente de las tasas de inversión de capital humano , del capital físico y del stock de conocimientos científicos básicos que existe . Este último, está expresado en el segundo término de la parte derecha de la ecuación (10’). De manera general, se considera que dicho término afecta de manera positiva a la productividad.
Ahora, retomando las ecuaciones (5) y (6), y si se considera que la economía aún no ha alcanzado el estado estacionario pero, que no está muy lejos de hacerlo, entonces, se puede obtener el crecimiento de la productividad entre dos periodos (t y t+w). Para ello, se construye una aproximación log-lineal al sistema formado por (5) y (6) en torno al estado de equilibrio. Esa hipótesis restrictiva de una proximidad del equilibrio estacionario nos llevará más adelante a analizar el carácter poco convincente, en el largo plazo, del modelo de Mankiw y alii (1992).
Comenzamos por definir algunas variables:
Dadas las expresiones anteriores podemos reescribir (5) y (6) de las siguientes maneras:
(5’)
(6’)
Al igualar y a cero, observamos que en el estado estacionario ha de cumplirse que:
(11)
Calculemos las
derivadas parciales de las dos expresiones extremas de la ecuación (11) con
respecto a  y
y  , respectivamente:
, respectivamente:
(11.1)
(11.2)
(11.3)
(11.4)
De las ecuaciones anteriores, podemos derivar las siguientes expresiones:
Ahora, haciendo uso de la fórmula de Taylor para aproximar y en torno al punto y , y dado que
Donde: , e representa la desviación de y con respecto a su estado estable .
De las expresiones anteriores, tenemos:
Ahora se obtienen:
(12)
(13)
Considerando este sistema, resulta sencillo analizar la evolución del producto por unidad de trabajo eficiente.
Dado que , tenemos la siguiente expresión:
y, reemplazando las ecuaciones (12) y (13) en esta última obtenemos:
ó
(14)
donde :
, y constituye la velocidad de ajuste.
Dado que (14) es una ecuación lineal, su solución es rápida, si se considera el periodo t a t + w, el valor al final del periodo de y estará determinado por una media ponderada de sus valores de principio de periodo y estacionario , con ponderaciones determinadas por el valor de b. Y, la ecuación que relaciona la derivada de la renta per cápita con su nivel en el estado estacionario y en el momento (t) es:
(15)
y, reemplazando la ecuación (10) en la (15), obtenemos:
(15’)
Esta ecuación nos indica que el producto por unidad de trabajo eficiente converge asintóticamente a su valor estacionario a una tasa exponencial (b) que está determinada por el grado de rendimientos a escala en los factores acumulables y las tasas de crecimiento de la población, del progreso técnico y de la depreciación.
Ahora, considerando que esta ecuación (15’), al igual que la ecuación (10), está escrita en términos de una variable (producto por unidad de trabajo eficiente) que no es observable directamente, es conveniente escribirla en términos por trabajador, es decir (producto por unidad de trabajo):
Para ello, recuérdese que: \
y aplicando logaritmo, tenemos:
de allí, se obtiene:
y sustrayendo en ambos lados, obtenemos la ecuación de convergencia condicional del modelo de Mankiw y alii (1992):
(16)
Ahora bien, cabe aclarar que las ecuaciones (10’) y (16) son similares a las que utilizan Mankiw y alii (1992) y son aquéllas que se utilizan en caso de que el indicador que se dispone para evaluar el capital humano refleja un flujo (por ejemplo, ratio de frecuentación o de inscripción). En caso contrario, es decir, si el indicador que se dispone para evaluar el capital humano representa un stock (por ejemplo, tasas de alfabetización), las ecuaciones (10’) y (16) se escriben de manera diferente.
En el caso del modelo de Mankiw y alii (1992), que aquí nos interesa, las ecuaciones utilizadas son las (10’) y la (16), es decir, se utiliza una proxy -(porcentaje de personas en edad de trabajar que están matriculadas en educación secundaria)- que representa un flujo de capital humano.
Además, Mankiw y alii (1992) parten del siguiente valor: ; de la consideración de una tasa de progreso técnico común para todos los países de la muestra considerada, es decir, de un término idéntico a todos los países en el nivel inicial de la tecnología y por otro idiosincrásico autónomo de las variables independientes (más adelante analizaremos este punto); de la hipótesis de rendimientos constantes a escala; de rendimientos decrecientes tanto en el capital físico como en el capital humano; se refieren a estimaciones cross-sección (sección transversal) para sus diferentes muestras.
II ) Resultados empíricos de estimación del modelo de Mankiw y alii (1992).
Algunos de los resultados empíricos de las estimaciones de Mankiw y alii (1992) se pueden observar a partir de los siguientes cuadros:
Cuadro 2. Test For Conditional Convergence [Tests for Conditional Convergence Restricted Regresión].
Variable dependiente: log PIB por persona en edad de trabajar (1960-1985)
|
Categorías |
Países no petroleros |
Países Intermediarios |
Países De la OCDE |
|
Observaciones: |
98 |
75 |
22 |
|
Ln (Y60) |
-0.289(0.062) [-0.299(0.061)] |
-0.366(0.067) [-0.372(0.067)] |
-0.39(0.70) [-0.402(0.069)] |
|
Implied l |
0.0137(0.0019) [0.0142(0.0019)] |
0.0182(0.0020) [0.0186(0.0019)] |
0.0203(0.0020) [0.0206(0.0020)] |
|
Implied a |
[0.48(0.07)] |
[0.44(0.07)] |
[0.38(0.13)] |
|
Implied b |
[0.23(0.05)] |
[0.23(0.06)] |
[0.23(0.11)] |
Los valores entre [ ] se refieren al modelo de Solow ampliado y las ( ) a los errores estándar.
FUENTE: MANKIW y alii (1990).
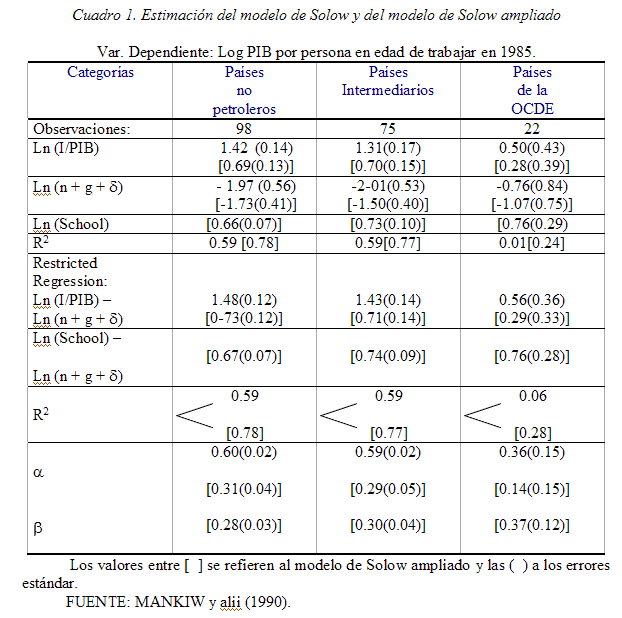
Primero y antes que nada, Mankiw y alii (1992) –partiendo de los “Penn Tables” construidos por Summers y Heston- proceden a estimar el modelo simple de Solow-Swan (1956) para tres subgrupos de países: 1) 98 países no petroleros, 2) 75 países intermediarios y 3) 22 países de la OCDE.
En el caso de los países de la OCDE los resultados nos muestran un valor de (0.5) para el coeficiente estimado del capital físico (es decir, la elasticidad de largo plazo del producto per cápita con respecto a s), un coeficiente de determinación del orden de (0.06) y una participación del capital físico de (0.36) (Ver Cuadro 1).
En lo que respecta a los subgrupos de los 98 países no petroleros y los 75 países intermediarios, la participación del capital físico en el producto es idéntica (0.6). Este valor es ligeramente mayor, respecto al valor –que bajo los supuestos de competencia perfecta, de ausencia de externalidades y con rendimientos constantes a escala- de 1/3 que parece ser compatible con las estimaciones empíricas, es decir, la observación de que en los países, la parte del producto pagado al capital es de aproximadamente 1/3.
Ahora, en el caso de los países de la OCDE, los resultados obtenidos a partir del modelo Solow-Swan simple de Mankiw y alii (1992) no son del todo válidos, dado que los hechos estilizados en torno a la hipótesis de convergencia entre los países industrializados nos indica una velocidad de convergencia del orden de 2% y no de aproximadamente de 4.5%, como se obtiene al considerar un a de aproximadamente 1/3. En efecto, para hacer compatible el modelo neoclásico con el hecho de que la velocidad de convergencia es del orden del 2% y, por lo tanto, considerar una participación del capital en el producto mayor –al 1/3 que predice el modelo neoclásico tradicional-, comprendido en un tenedor de (0.75-0.80), en la literatura sobre crecimiento económico y convergencia hay dos mecanismos disponibles. La primera -retomada por Romer (1987)-, considera la posibilidad de importantes externalidades positivas asociadas con la acumulación del capital. La segunda, considera la posibilidad de incluir otras variables a la regresión, como por ejemplo, capital humano y tecnológico, y así, argumentar a favor de un capital relevante cuya participación en el producto resultara mayor que la participación del simple capital físico.
Aquí, en este trabajo, consideramos el segundo mecanismo, dado que Mankiw y alii (1992) incluyeron la variable capital humano como una variable adicional al modelo de Solow-Swan con el fin de acercar los valores de los coeficientes y las participaciones del capital físico con aquellos valores que predice la teoría –es decir, reducir la sobreestimación del rendimiento del capital físico en el caso de los subgrupos de países: no petroleros e intermediarios, y procurar aproximar alrededor de 0.75 la participación del capital relevante- y mejorar aún más la capacidad explicativa del modelo.
Efectivamente, al incluir la variable capital humano en el modelo de Solow-Swan (1956) (Ver Cuadro 1) se hicieron coherentes las pruebas con la conclusión inicial de Solow-Swan y de ciertos trabajos empíricos en torno al rendimiento del capital físico que se evidencia en una tercera parte del producto. La introducción del capital humano es significativa y su tamaño (coeficiente) es de 0.76, además, mejora el ajuste del modelo de Solow-Swan que ahora es igual a 0.28 para el caso de los países de la OCDE.
Los resultados son aún más sorprendentes para el caso de los países intermediarios y los países no petroleros; el coeficiente del capital humano es de 0.6 y 0.7, respectivamente; el rendimiento del capital físico es de 0.31 y 0.29, respectivamente (recuérdese que antes era de 0.60); por su parte, la capacidad explicativa es de 0.78 y 0.77, respectivamente.
Otro aspecto relevante que hay que rescatar con la introducción del capital humano es el relacionado con la convergencia económica. En efecto, de acuerdo a la evidencia empírica que sustenta la hipótesis de convergencia se estima una velocidad de convergencia que se encuentra en un tenedor de (0.015 - 0.03) y, por lo tanto, de una participación del capital relevante alrededor de 0.7 y 0.8.
De manera general, podemos decir que las estimaciones de Mankiw y alii (1992) son coherentes con las predicciones anteriores dado que las elasticidades de los factores de producción son: b = 0.23 y a comprendido entre (0.38 y 0.48). (Ver Cuadro 2).
La participación del capital relevante, representado por la sumatoria (a + b) está entre (0.6 y 0.7), y el valor promedio de la tasa de convergencia, es decir, la tasa de convergencia del subgrupo compuesto de 98 países, hacia su sendero de crecimiento es de 1.4%. Además, el coeficiente del ingreso per cápita inicial es negativo (-0.29) y estadísticamente significativo. Esos mismos resultados se observan en los otros subgrupos de países. En el caso de los países de la OCDE la convergencia se realiza al ritmo de 2% anual.
En suma, la concordancia de los resultados del modelo Mankiw y alii (1992) con los hechos estilizados sobre crecimiento y convergencia económica sugieren que un modelo que adopta una definición amplia del capital de tal suerte que su participación es de alrededor de 0.7 –en vez de únicamente el capital físico, como se procede en el modelo simple Solow-Swan (1956)- y que además hace suya la hipótesis de rendimientos decrecientes del capital, parece proporcionar una buena aproximación de los datos de corte transversal y nos deja ver bien claro que el capital humano tiene un lugar legítimo en la función de producción agregada y que, además, su contabilización conjunta con el capital físico nos esclarece en torno a las grandes diferencias en los niveles de ingreso observados en corte entre los países. Este último punto se puede ilustrar muy fácilmente: si consideramos las siguientes elasticidades: a = 0.36 y b = 0.42 y si partimos de la ecuación (10’) esos valores implican que las elasticidades de la producción con respecto a y serán de 1.6 y 1.9, respectivamente. En el caso del modelo Solow-Swan (1956) donde no hay capital humano, si a = 0.36, la elasticidad de la producción con respecto a sK sería de 0.56. Dados esos resultados se puede considerar que el modelo de Mankiw y alii (1992) está mejor dotado, como habíamos mencionado antes, que el modelo de Solow-Swan (1956).
Sin embargo, a pesar de los resultados Mankiw y alii (1992) analizados, dicho modelo ha estado sujeto a muchos cuestionamientos ya que no ha podido explicar muchos hechos estilizados, tales como por ejemplo: -si bien el modelo hace suyo la hipótesis de rendimientos marginales decrecientes en el capital físico y humano, lo que por consiguiente, como ya se sabe, debe implicar un menor rendimiento del capital físico y humano en los países ricos con respecto a los países pobres- ¿por qué el capital no se dirige hacia los países del sur?. Otro problema fuerte del modelo para algunos consiste en su robusticidad y la sesgabilidad de sus coeficientes.
III ) Algunos trabajos y resultados empíricos inspirados a partir de
Mankiw y alii (1992)
En lo que sigue analizaremos algunos trabajos en los cuales se ponen a prueba y se analizan las fallas del modelo Mankiw y alii (1992).
Kauffmann( 2002) utiliza una especificación idéntica a la que utiliza Mankiw y alii (1992), con algunas modificaciones importantes: 1) utiliza dos bases de datos alternativos: una que principia en 1880 y que se restringe a los países desarrollados y la otra base de datos incorpora a los países de América Latina, pero principia a partir de 1920; 2) analiza a 10 países de la OCDE en panel sobre un periodo de 100 años, es decir, 1880-1980. Recuérdese que en el caso de Mankiw y alii (1992) se utiliza un periodo de 25 años con una estimación de sección transversal respecto a 22 países de la OCDE; 3) utiliza como variable endógena la tasa de crecimiento dividida entre la población total; en el caso de Mankiw y alii (1992) se utilizó tasa de crecimiento dividida entre la población activa; y 4) utiliza como capital humano una tasa de escolarización en la primaria y en la secundaria; en el caso de Mankiw y alii (1992) se utilizó el porcentaje de los estudiantes del nivel de secundaria en la población activa.
A continuación, reportamos algunos resultados de regresiones que figuran en el trabajo de este autor.
Cuadro 3. Especificación de Mankiw, Romer y Weil (1992)
|
|
Aplicada a la base 1880-1980
Ln(escol. act) Ln (escol. 10) |
Aplicada a la base 1920-1980
H: Ln(escol. H: Ln(escol. 10) actual) |
||
|
Ln (y) |
0.020** (0.004) |
-0.024**(0.005) |
-0.042**(0.011) |
-0.055**(0.013) |
|
Ln (Inv) |
-0.01 (0.004) |
0.01(0.004) |
|
|
|
Ln(escol.) |
0.12* (0.007) |
0.018**(0.007) |
|
|
|
Ln(n +0.05) |
-0.229**(0.084) |
-0.294**(0.089) |
0.278**(0.075) |
0.308**(0.074) |
|
H |
|
|
-0.035(0.008) |
-0.018**(0.008) |
|
R2 |
-0.255 |
0.270 |
0.362 |
0.444 |
|
Numero de observs. |
810 |
710 |
912 |
722 |
Variable dependiente: Ln yi,t+1 – Ln yi t ; Ln y: ingreso inicial per cápita; Ln (Inv): Log de la inversión; Ln (School): Log de la educación; n: tasa de crecimiento demográfica; 0.05: a proxy de la suma de la tasa de depreciación y del progreso técnico; H: Log de la educación; desviación estándar entre paréntesis; significatividad de los coeficientes a 5% (**) y 10% (*); Ln (escol. Actual): Log de escolarización actual como indicador del capital humano; Ln (escol. 10): Log de escolarización retardada de 10 años.
FUENTE: Kauffmann (2002).
En efecto, a raíz de las modificaciones mencionadas arriba –reconocidas por el autor- no es posible hacer una comparación de número a número; sin embargo, se pueden apreciar y hacer algunas interesantes observaciones:
v Un reducido efecto de la variable capital humano en los resultados de este autor, en comparación a los resultados obtenidos en la estimación de Mankiw y alii (1992). Si bien es cierto que el coeficiente del capital humano, en la muestra relativa a los 10 países de la OCDE utilizada por Kauffmann (2002), es positivo y significativo, pero es muy reducido en comparación al valor obtenido en Mankiw y alii (1992). Este resultado es interesante dado que contradice la mayoría de los resultados de los estudios realizados sobre datos de panel –que en algunos casos arrojan una falta de significatividad del capital humano en las ecuaciones sobre crecimiento económico y en otros casos arrojan una relación significativa pero negativa entre el capital humano y el crecimiento-. Ese extraño resultado contradictorio podría deberse al hecho de que la muestra de los 10 países de la OCDE está compuesta por países relativamente homogéneos (al contrario de los demás estudios sobre datos de panel que suelen incluir grandes cantidades de países heterogéneos en sus muestras), que se ubican en una región específica, que tienen los mismos comportamientos de acumulación, por lo tanto, las diferencias observadas se traducirían por los distintos niveles de crecimiento en torno al stock de capital humano o en torno a la inversión en capital humano.
Esa diferencia entre los resultados de esas dos estimaciones sugiere un impacto de sección cruzada de la variable educación mayor que el efecto temporal obtenido, es decir, el capital humano permite clasificar mejor a los países entre sí, en vez de explicar sus evoluciones temporales.
v El efecto negativo del capital humano sobre el crecimiento económico y el efecto positivo sobre el crecimiento de la sumatoria entre .
Las razones de esos cambios pueden deberse a diferentes motivos:
1) por incluir países heterogéneos (países de América Latina) a la muestra
2) por optar por un modelo con efectos fijos, en vez del Modelo de Mínimo Cuadrado Ordinario
3) por no incluir a la variable inversión, y por reducir el periodo analizado, que es de 60 años (1920-1980). Ese cambio y esa omisión (sobre todo) es debido a la ausencia de datos sobre inversión para el caso de los países de América Latina antes del año de 1920 y de los malos resultados obtenidos respecto de la variable inversión para el caso de los países de la OCDE y de la demostración del carácter indolor de la variable inversión en el seno del modelo (que excluye a los países de América Latina) -es decir, el modelo estimado previamente-, para el periodo de 1880-1980.
Para Kauffmann (2002), tal parecería que no es la agregación de los países de América Latina que explican esos resultados -porque si tal fuese el caso, su no inclusión en una estimación en un modelo sobre un periodo similar (1920-1980) no debería producir los mismos resultados; groso modo Kauffmann (2002) nos dice que parece que con o sin los países de América Latina los resultados son idénticos- más bien lo que parece explicar esas divergencias de resultados es la reducción de la dimensión temporal.
Es a partir de esas estimaciones que Kauffmann (2002) subraya el carácter poco convincente a largo plazo del modelo de Mankiw y alii (1992). Concluye considerando que la robustez de dicho modelo se verifica principalmente sobre el periodo de post-guerra (1960-1985) y que la reducción del horizonte temporal de la base de datos, con la agregación de los países de América Latina conducen a resultados sorprendentes. Además, considera que a esa falta de robustez se añade (lo que ya habíamos mencionado anteriormente) la restricción de proximidad de los países, de su estado estacionario, lo que es muy incómoda y creíble en el caso de un estudio a largo plazo.
Ángel de la Fuente y Juan Francisco J. Serrano (1999), partiendo de una muestra de 110 países para el periodo (1960-1985), con datos retomados de Summers y Heston realizaron dos ejercicios interesantes.
En el primer caso, reestimaron el modelo de Mankiw y alii (1992) –anexándole la variable school construidos por ellos- con datos de sección transversal y utilizando, tanto el método de mínimo cuadrado ordinario como el método de mínimos cuadrados no lineales, y llegaron a la conclusión de que los valores estimados de los parámetros –de sus resultados- son razonables y son parecidos a los (resultados) de Mankiw y alii (1992). Entre otros, destacaron:
- el papel importante en el crecimiento del capital físico y humano
- la significatividad y la negatividad del coeficiente de la renta inicial, lo que, por lo tanto, sostiene la hipótesis de convergencia condicional
- la capacidad del modelo para explicar, de manera razonable, la magnitud observada de las diferencias de renta entre países.
En el segundo caso, reestimaron el modelo de Mankiw y alii (1992) –anexándole la tasa de escolarización secundaria, retomada de Barro y Wolf (1989)- con datos de panel y desagregando la muestra en dos sub-periodos: 1960-1975 y 1975-1985. Los resultados a los cuales llegaron, ahora son muy diferentes:
- una tasa de convergencia por debajo de la obtenida con los datos de sección transversal
- valor del coeficiente del capital físico muy superior al sugerido por las estimaciones empíricas
- la pérdida de significatividad del capital humano.
A raíz de los resultados anteriores, De la Fuente y al (1999) subrayaron al menos dos aspectos en los que el modelo de Mankiw y alii (1992) no resulta satisfactorio:
“El primero es su incapacidad para explicar la variación en el tiempo de la tasa de crecimiento. Puesto que la inversión en capital físico no ha variado demasiado y las tasas medias de escolarización han aumentado considerablemente, la ralentización del crecimiento en la segunda mitad del periodo muestral ha de atribuirse a algún factor no recogido por el modelo (...) En segundo lugar, ... La falta de significatividad de esta variable [capital humano] ... parece deberse a que la tendencia positiva de los niveles de escolarización recoge la caída de la tasa de crecimiento. Una vez se introduce una variable ficticia para controlar este efecto, la inversión en capital humano vuelve a entrar en la ecuación con el signo esperado.” (De la Fuente y al, 1999: 99-100)
A manera de conclusión se tiene que para De la Fuente y al (1999) la no satisfacción del modelo de Mankiw y alii (1992) es debido a la omisión de variables relevantes en el modelo.
Grossman y Helpman (1991, 1994) criticaron el modelo de Mankiw y alii (1992) por considerar una tasa de progreso técnico común a todos los países. Consideran que si el progreso técnico no es común a todos los países y además sus variaciones son tratadas como formando parte del término estocástico no observado, entonces el uso de los mínimos cuadrados ordinarios para estimar las ecuaciones dará por resultados estimaciones sesgadas cuando hay correlación entre las razones inversión/PIB y el crecimiento económico de cada país específico. De manera peculiar, consideran que si son elevadas las tasas de inversión cuando se incrementa la productividad, el coeficiente de la variable de inversión tomará una parte de la variación que es debido a sus experiencias distintas de progreso técnico. Además, consideran que la inversión sería más alta allí donde el incremento de la productividad es mayor.
Lo anterior implica que las estimaciones obtenidas por Mankiw y alii (1992) en torno al efecto de la variable inversión están sobreestimadas. De acuerdo con Pierre Richard Agenor (2000), a pesar de que el tamaño de ese sesgo aún no ha sido evaluado de manera precisa, se considera que está relacionado con la capacidad del modelo para explicar las diferencias de cortes de los niveles de ingreso y no las diferencias de las tasas de crecimiento.
Adolfo Gutiérrez de Gandarilla Saldaña y Ana López Martínez (1998), estilizando la especificación de Mankiw y alii (1992) para una muestra de 9 países de la Unión Europea (UE) para dos periodos: (1960-1990) y (1960-1995) con datos obtenidos de los Statistics Direction National Accounts de la OCDE, de Eurostat y de los Statistical Yearbook de Naciones Unidas y de la UNESCO, consideran que los valores resultantes de sus regresiones se mantienen en la misma línea de los valores estimados a partir del modelo de Mankiw y alii (1992), por lo consiguiente, señalan que cuando se incluye un horizonte temporal más amplio no se pierden los atributos explicativos imputados al capital humano.
Barro, Mankiw y Sala-I-Martin (1995) hicieron una crítica a nivel conceptual del modelo de Mankiw y alii (1992) y lo reestimaron al incluirle una movilidad parcial del capital físico y al suponer que parte del stock de capital físico es utilizado como colateral de los préstamos en los mercados internacionales de capitales. A raíz de esa modificación obtuvieron la siguiente fórmula de tasa de convergencia:
Islam Nazrul (1995), partiendo de la hipótesis de una tasa de progreso técnico común (idéntico) a todos los países, de un enfoque en términos de datos de panel al modelo de Solow y utilizando las mismas regresiones de Mankiw y alii (1992) sobre otras muestras, obtuvieron resultados muy diferentes a aquellos obtenidos por Mankiw y alii (1992). Su metodología permite:
1) obtener parámetros de la función de producción diferentes de un país a otro.
2) “obtener estimaciones de las diferencias en la productividad total de los factores que harían que un modelo de Solow ... diera cuenta de las diferencias internacionales observadas en los niveles de ingreso y las tasas de crecimiento”. (Ros, Jaime, 2001: 14)
3) “... (por comparación) de eliminar el efecto de la variable inobservable [eficiencia inicial técnica]”. (Philippe Aghion, Peter Howitt, 1998: 37)
Este tercer punto es importante, dado que la eliminación (por comparación) del efecto de la variable inobservable cambia drásticamente los resultados que se acostumbra obtener respecto a la convergencia.
Otro resultado importante del modelo de Islam (1995), es que ahora la productividad total de los factores capta lo que era atribuido al capital humano en el modelo de Mankiw y alii (1992)[4].
Klenow P. y A. Rodríguez-Clare (1997b)[5], a partir de una metodología basada en Mincer para medir el capital humano, reexaminaron la metodología que utilizaron Mankiw y alii (1992) para descomponer los factores que determinan el crecimiento. Además, para medir el capital humano, utilizan las matrices en educación primaria, secundaria y universitaria –se recordará que Mankiw y alii (1992) únicamente utilizaron la educación secundaria.
Encontraron, al igual que Easterly y Levine (2000) –como veremos a continuación-, que las diferencias en los residuos (productividad total de los factores) –para una muestra de 98 países en el periodo 1960-1995- explicaron alrededor del 90% de las diferencias en el producto por habitante[6].
Easterly y Levine (2001)[7], partiendo de los supuestos de: 1) función de producción Cobb-Douglas; 2) elasticidad capital-producto constante (fijada a 0.4); 3) rendimientos constantes a escala; 4) progreso técnico Hicks neutral; y 5) tecnologías diferentes entre los países y utilizando una de las especificaciones de Mankiw y alii (1992) cuantifican para unos países los papeles respectivos de la productividad total de los factores y del capital. Los resultados de su examen destacan la importancia del rol fundamental de los residuos de la productividad para explicar los logros económicos. Además consideran que el modelo neoclásico no explica de manera adecuada la complejidad de los hechos estilizados del proceso de crecimiento económico, salvo en las economías industrializadas.
Benhabid J. y Spiegel M. M. (1994) haciendo uso, especialmente de los años medios de escolarización como proxy del capital humano, de los datos de Kyriacou (1991) y modificando ligeramente la clásica función de producción Cobb-Douglas –generalmente presentada en cuestiones de crecimiento con capital humano- con información de sección transversal para más de 70 países, terminaron por concluir:
- que los países que más han acumulado capital humano durante el periodo (1965-1985) no tuvieron por ello un crecimiento más rápido y que no se han observado pruebas de algún efecto directo de la acumulación del capital humano sobre la productividad. Sus resultados indican –únicamente- que la tasa de crecimiento está relacionada con el nivel inicial de la proxy del capital humano.
Esas conclusiones de los autores dejan muchas dudas sobre la robustez del modelo de Mankiw y alii (1992) y sugiere que –a la excepción de los países desarrollados– se debería, en las muestras utilizadas en los modelos, distinguir grupos de países con tecnologías diferentes o comportamientos disimilares.
Kyriacou (1991), Romer (1989a), Lee, Pesaran y Smith (1996), Cho y Graham (1996), Berthélemy, Dessus, Varoudakis (1997), en sus trabajos empíricos, de cierta manera, apoyan la tesis anterior en el sentido de que no se ha observado –como sucede en el modelo de Mankiw y alii (1992)- un efecto directo de la acumulación de la proxy del capital humano sobre el crecimiento económico.
Levine y Renelt (1992). A raíz de la amplia gama de estudios sobre crecimiento económico (que abarcan grandes cantidades de países sobre diferentes periodos, incluyendo un sin fin de variables explicativas, con el fin de ver su correlación con el crecimiento y que además brillan por una ausencia de base teóricos explícitos y, por lo consiguiente, de grandes cantidades de conclusiones dispares), se ha tornado extremadamente difícil generalizar o tomar como viable y fiable algún o algunos estudios en particular. Por ello, Levine y su coautor (1992) realizaron una revisión metodológica y conceptual con el fin de averiguar la robustez estadística de las correlaciones –entre esas grandes cantidades de variables explicativas, y el crecimiento- que figuran en esa literatura.
Para llevar acabo su cometido, utilizaron la metodología de “límites extremos”[8] recomendado por Leamer (1983, 1985). Dentro de sus hallazgos[9] encontraron que, salvo la tasa de inversión en capital físico, el PIB inicial y la inversión en capital humano, la correlación parcial de las demás variables con el crecimiento económico no era robusta a cambios de especificaciones. Además, recalcaron que la robustez de la correlación entre crecimiento económico y la proxy del capital humano (es decir, la escolarización secundaria) se mantenía, siempre y cuando no se integraban otros regresores en la regresión.
Grosso modo, esos hallazgos de Levine y Renelt (1992) básicamente nos indicaban un escenario no prometedor y además, que estuviésemos lejos de obtener resultados viable y fiables de los parámetros claves de las distintas especificaciones en los modelos que figuran en el programa de investigación neoclásico[10]. Utilizamos el pasado simple dado que –de manera tímida y aún no concluyente como lo apunta P. R. Agenor (2000))- la literatura reciente ha destacado que:
- Tanto la inversión en educación como el capital humano permite adquirir competencia que aumente la eficacia e incremente el ritmo de la intensidad del uso de las tecnologías existentes.
- Un nivel inicial de educación es un determinante relevante para el crecimiento futuro.
- Una mejor educación y un mayor gasto público en educación, como porcentaje del PIB, eran favorables al crecimiento.
- La calidad de la educación era importante para el crecimiento.
Algunas Consideraciones
A pesar de las críticas a las cuales fue sometido el modelo de Mankiw y alii (1992) –como pudimos apreciar en el sucinto seguimiento de algunos trabajos publicados durante la década 90 y en el amanecer de este siglo, examinados arriba- se debe considerar que dichos trabajos críticos son muy dispares: no se constituyen sobre hechos de observación derivados de periodos de tiempo homogéneos entre sí; se constituyen sobre grandes diferencias conceptuales y bases de datos agregados que disfrazan buena parte de la realidad; su elección de buenos indicadores es un rompecabezas no resuelto; sus resultados empíricos no son definitivos; sus conclusiones no permiten elaborar un mensaje global; no forman un bloque sólido; carecen de una herramienta metodológica estadística (econométrica) que hacen la unanimidad entre los autores; grosso modo, no son universalmente concluyentes, y no constituyen aportes revolucionarios en cuestiones de crecimiento en el seno del programa de investigación neoclásico. Por lo consiguiente, es difícil considerar que pueden invalidar empíricamente el modelo neoclásico en la versión Mankiw y alii (1992) dado que este modelo introduce inteligibilidades en la disciplina económica. Más bien creemos que deben ser considerados como aportes evolucionarios y que también introducen ciertas inteligibilidades en la ciencia económica.
Consideramos lo mencionado arriba, por el simple hecho que si miramos minuciosamente de cerca la historia de los modelos de crecimiento del programa de investigación neoclásico, no siempre se han considerado las desmentidas de los hechos estilizados. Además, podemos señalar –sin temor a equivocarnos- que han evolucionado (por lo menos hasta cierto punto) gracias a esa negligencia. Para ilustrar lo dicho anteriormente, basta recordar lo que sucedió entre 1985-1990 en nuestra disciplina con la llegada de los nuevos modelos de la teoría del crecimiento endógeno que postulaba el supuesto de rendimientos crecientes y constantes y que dio lugar a ponerlo en tela de juicio y a una sensación de rechazo del modelo neoclásico a la Solow-Swan (1956) por postular el supuesto de rendimientos decrecientes en el capital y la tesis de convergencia convencional absoluta entre los países. Sorpresivamente, en el momento en que se manifestaba esa sensación de rechazo del modelo de Solow-Swan (1956), cuatro trabajos de algunos ilustres economistas (Young (1994), Barro (1991), Barro y Sala-I-Martin (1992) y Mankiw y alii (1992)) lo rescataron, lo hicieron evolucionar. Incluso, el mismo Romer -quien principió con esas críticas y que no consideraba a la hipótesis de convergencia como un hecho de observación, recomendó reemplazar el supuesto de rendimientos decrecientes por el de rendimientos crecientes- vio debilitar ese último supuesto o por lo menos ponerlo en tela de juicio, dado que otros autores han considerado que con este supuesto, las economías con grandes stocks de capital deberían experimentar un crecimiento explosivo, hecho que por supuesto no se ha observado[11].
Grosso modo, nos queda recalcar que si bien las disputas en nuestro gremio entre los diferentes modelos de crecimiento nos dejan la sensación que son antagónicos, creemos que esos modelos deben considerarse como parciales, complementarios y evolutivos, que permiten ciertas inteligibilidades en ese tema tan complejo como es el determinar los diferentes factores que explican el proceso de crecimiento económico, y que aún siguen persistiendo muchas preguntas sin respuestas, las cuales dejan un gran lugar en la agenda de la investigación económica para futuros trabajos sobre crecimiento económico y convergencia, en el seno del Programa de Investigación Neoclásico.
[1] Entusiasmado por los artículos de Weintraub (1985), Heijdra y Lowenberg (1988) y sobre todo el de Marc Lavoie (1991), quien retomó de Imre Lakatos (1975) su concepto de Programa de Investigación, consideró que el Programa de Investigación Neoclásica tiene cuatro premisas fundamentales: 1) el individualismo metodológico, 2) una epistemología instrumentalista, 3) la búsqueda de una asignación óptima de las dotaciones, y 4) una racionalidad ilimitada; y está constituido por dos grandes ramas: 1) la del equilibrio general, que a partir de construcciones axiomáticas suministra los fundamentos al programa de investigación neoclásica, y 2) la del equilibrio parcial y la macroeconomía, que provee los campos en donde la economía neoclásica puede expresarse sobre cuestiones concretas.
Para Weintraub (1985) y Marc Lavoie (1991), la Teoría del Equilibrio General es el núcleo duro de dicho programa, mientras que las teorías macroeconómicas y los enfoques de equilibrio parcial se encuentran en su capa protectora (el semi-núcleo). Siguiendo a Marc Lavoie (1991), el semi-núcleo se aplica a la versión vulgar de la economía neoclásica, la que se encuentra en todos los manuales en los trabajos empíricos y en macroeconomía. Los modelos derivados de dicha capa protectora se aglutinan para formar teorías, sea por campo de adhesión (economía pública, crecimiento y desarrollo económico, etc.), sea por afiliación (monetaristas, nuevos keynesianos, nuevos clásicos, etc.).
[2] · Es un operador que nos indica la derivación respecto al tiempo (d/dt).
[3] Las variables evaluadas en el estado estacionario se nomenclaturan con *
[4] Respecto a este punto, ver J. Ros pp. 14 y 15.
[5] Esta parte está inspirado en los trabajos de Jaime Ros (2001) y Francisco Rosende (2000).
[6] Cabe mencionar que una crítica de la medición del capital humano utilizada por Klenow y Rodríguez-Clare (1997) ha sido realizada por Mankiw (1997).
[7] Sintetizan en cinco, los hechos utilizados en el ámbito del crecimiento económico:
1. En vez de la acumulación de los factores, es la de los residuos que explica la mayoría de las diferencias de crecimiento y de ingreso a través de ratios.
2. A largo plazo los ingresos divergen.
3. Se observa una persistencia de la acumulación de factor, mientras que el crecimiento no lo es, es decir, no es persistente.
4. Hay una fuerte concentración de la actividad económica, todos los factores de producción y principalmente humanos van hacia las zonas más ricas.
5. Las políticas en el ámbito nacional ejercen una gran influencia sobre los regímenes de crecimiento económico.
[8]Ese test considera 4 tipos de variables, una independiente y tres dependientes: esas últimas se clasifican como: variable de interés directo, variables llamadas dudosas y variables libres, y consiste en rotar a la vez la variable de interés y las libres –que siempre figuran en el conjunto de información- con las variables dudosas (que por cierto, van cambiándose en las distintas especificaciones). Si el coeficiente de la variable de interés directo no pierde su significancia y guarda el signo esperado en todas las distintas especificaciones, se considera robusta la correlación parcial entre la variable dependiente y la variable de interés directo.
Cabe agregar que el análisis de “límites extremos” ha sido sujeto a amplias críticas (Ver Sala-I-Martin (1997)).
[9] De manera resumida, los resultados de sus hallazgos consisten en reconocer la falta de robustez estadística de las correlaciones parciales entre más de 50 variables explicativas y el crecimiento dentro de la literatura empírica sobre crecimiento económico y en poner en tela de juicio la validez de los modelos de crecimiento económico –sobre todo aquellos modelos ad hoc que no tienen ninguna base teórica sólida- utilizados en nuestra disciplina.
[10] Además de lo explicado anteriormente sobre el Programa de Investigación Neoclásico (nota 1), es oportuno: 1) recalcar que tanto el núcleo duro como el semi-núcleo de dicho programa tienen sus postulados fundamentales, sus heurísticas, sus reglas de conducta, y 2) esgrimir, de acuerdo a Marc Lavoie (1991), y sin ser exhaustivos, sus elementos.
1. Los postulados encuadrados en el núcleo duro son: i) los agentes tienen dotaciones (en bienes o en servicios productivos) fijos; ii) existe un conjunto de producción; iii) los agentes tienen preferencias; iv) los agentes son racionales, i.e., optimizan bajo restricción; v) no hay comportamiento de grupo, i.e., solamente existen agentes que actúan de manera independiente; vi) los agentes tienen un conocimiento correcto; vii) existen mecanismos que aseguran la coordinación de las decisiones.
2. Las reglas de conducta aglutinadas en el núcleo duro son: 1) demostrar la existencia del equilibrio; 2) demostrar la unicidad del equilibrio; 3) demostrar la estabilidad del equilibrio; 4) demostrar la optimalidad del equilibrio; 5) establecer las condiciones suficientes para la realización de las reglas “1 al 4”; 6) completar el modelo, aún cuando las condiciones parecen irrealistas; 7) tomar siempre como punto de referencia el equilibrio walrasiano, aún cuando la regla 2) no ha podido ser verificada; 8) interpretar o comprender el mundo real a partir del modelo de equilibrio general completo; 9) introducir cierto realismo, al omitir o al reemplazar ciertas de las condiciones enunciadas en 5), al someterse de nuevo a las reglas “1 al 6”.
3. Los postulados que integran el semi-núcleo son: i) existen siempre las posibilidades de sustitución en las elecciones de los agentes; ii) existen siempre las posibilidades de sustitución a nivel de las técnicas de producción; iii) la ley de los rendimientos decrecientes se aplica a cualquier tiempo; iv) cada agente maximiza su utilidad o su beneficio; v) existe un mercado para cada input y output; vi) el equilibrio es el encuentro de una oferta y de una demanda; vii) el precio es la principal variable de ajuste, o explicativa; viii) salvo imperfecciones o rigideces, el equilibrio es óptimo; ix) si la información es imperfecta, el caso siempre puede reducirse a una situación de riesgo probabilizable.
4. Las reglas de conducta que componen el semi-núcleo son: 1) el modelo neowalrasiano de equilibrio general representa el mundo idealizado; es el modelo de referencia; 2) suponer que la teoría del equilibrio general ha demostrado la existencia de un equilibrio único, estable y óptimo bajo ciertas condiciones; 3) postular que la teoría del equilibrio general justifica la representación simplificada adoptada; 4) postular que las simplificaciones escogidas para poder operar al interior de la capa protectora permiten evolucionar bajo las condiciones mencionadas en 2); 5) postular que los principales resultados obtenidos por las simplificaciones elegidas no deben ser cuestionados por un modelo de equilibrio más general o más completo; 6) adoptar el marco abstracto de la teoría del equilibrio general, tal como está definido por su núcleo y, además, integrar los elementos específicos del semi-núcleo; 7) llevar la noción de racionalidad económica y la capacidad de tratar la información tan lejos como sea razonablemente posible hacerlo; 8) introducir las instituciones o aspectos institucionales, pero al considerarlos como imperfecciones, 9) excluir del campo de estudio lo que no puede ser modelizado; 10) buscar un equilibrio estacionario o casi estacionario al estudiar diversas variantes.
[11] En el calor del debate en torno a que si la actividad científica no consiste únicamente en rechazar teorías o en corroborarlas, nació la postura –integradora de la visión positiva de Khun y normativa de Popper- de Programa de Investigación, concepto que fue acuñado por Imre Lakatos (1975), en donde se trata de ver qué es lo caracteriza a la ciencia.
De manera intuitiva, un Programa de Investigación es un principio heurístico basado sobre dos grandes ejes, de un lado, un núcleo central (duro), compuesto: de supuestos, de premisas, declarados irrefutables; de una heurística positiva que proporciona sugerencias, indicaciones que permiten cambiar, desarrollar, las variables refutables de dicho programa, es decir, desarrollar modelos cada vez más sofisticados con el fin de dar cuenta cada vez mejor de la realidad; y de una heurística negativa, que consiste en tratar de eliminar las anomalías que puede encontrar una teoría al modificar ciertas hipótesis auxiliares, es decir, a grandes rasgos nos dice qué senderos de investigación debemos evitar; y, por otro lado, de un cinturón protector que provee un conjunto de hipótesis auxiliares que pueden ser rechazadas. Esas hipótesis –partiendo de la heurística positiva- se van cambiando si son falseadas.
En cuanto al carácter evolutivo de los programas de investigación, Lakatos (1975) considera que toda nueva etapa de un programa de investigación debe ser caracterizada por un incremento del contenido empírico corroborado. Si es así, se dice que el programa de investigación progresa, en caso contrario, degenera y, por lo tanto, hay que abandonarla por otro, siempre y cuando que este otro explique el logro del primero y lo supere al desplegar un poder heurístico mayor.

