DISEÑO DE ELEMENTOS DE MÁQUINAS I

3.2.-FATIGA

• Es la reducción de la resistencia de un material debido a que sobre él actúan cargas fluctuantes (o cíclicas).
• Los elementos pueden fallar por acción de tensiones alternativas, aún sin llegar a valores críticos para esfuerzos estáticos, incluso a muy inferiores al límite de fluencia.
• La falla por fatiga empieza por una pequeña grieta, que se desarrolla por un cambio de sección, un chavetero, un orificio, en las marcas de fábrica e incluso irregularidades originadas por la mecanización.
• La grieta va aumentando progresivamente hasta que llega un momento en que el área o sección neta de trabajo es tan pequeña que la pieza se rompe repentinamente.

Su = limite de rotura.
Sy = limite de fluencia.                      
    = limite de fatiga.
Para el acero:
 (Ec. 3.2)                  sí          
Pero si:              entonces         
Para el Hierro fundido y bronce:       
 (Ec. 3.3)
Para casi todos los aceros se puede determinar gráficamente el Diagrama de Fatiga o Diagrama S-N, normalmente para estos materiales ocurre que para cada:

 

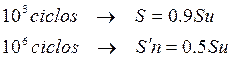
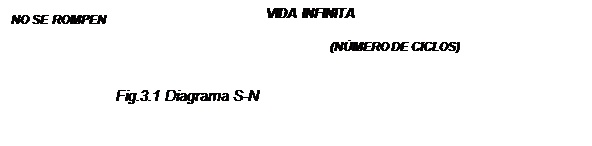
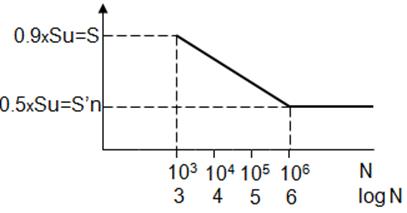
Supóngase que estamos probando una viga giratoria que fue cargada de tal manera que el esfuerzo está muy próximo al punto de cedencia (Su) del material, es decir, que con un esfuerzo de esta magnitud bastarían relativamente pocos ciclos para causar la falla. Pero si otra probeta se probara con un esfuerzo más bajo, veríamos que el número de ciclos necesario para romper la probeta aumentaría considerablemente.
EjemploN°3.3: Representar el diagrama S-N de un acero AISI C 1035, laminado en caliente del cual se ha hecho una probeta tipo viga giratoria, y encontrar la resistencia a la fatiga correspondiente a una vida de 82,000 ciclos.
Solución:
Según la tabla de propiedades el acero AISI C1035, tiene:
Sy=3,800 kg/cm2   y   Su=6000 kg/cm2
Por tanto:

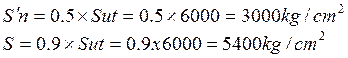
La resistencia a la fatiga para 82000c se obtiene a través de la siguiente relación:

 

 

 

 

 

 

 

 

 

 

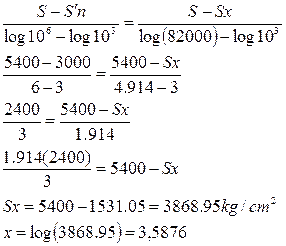
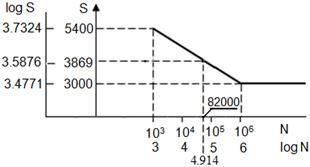
EjemploN°3.4: Un acero AISI 1045 tiene una resistencia a la tensión de 95 Kpsi y una resistencia de fluencia 74 Kpsi.

• Determinar el límite de fatiga de la viga giratoria.
• La resistencia a la fatiga correspondiente a 104 ciclos de duración.
• Estimar la duración correspondiente a un esfuerzo completamente invertido de 55 kpsi.

SOLUCIÓN:

• Para aceros

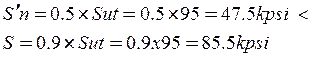
• Para 104 ciclos la resistencia a la fatiga es:

 

 

 

 

 

 

 

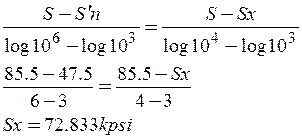
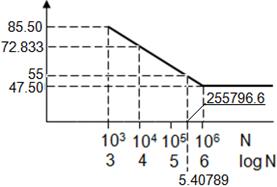
c) Para un esfuerzo de 55 Kpsi

 

 

 

 

 

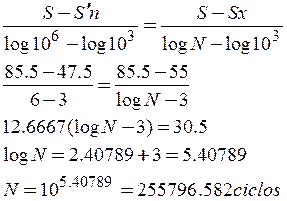
3.2.1 COEFICIENTES MODIFICATIVOS DEL LÍMITE DE FATIGA

El límite de fatiga de una pieza puede ser muy diferente al encontrado por el ensayo de R.R.Moore. Debido a que la pieza no tenga la superficie pulida, que tenga puntos de concentración de tensiones, o que opera a alta temperatura.  Por esto se ha sugerido emplear “coeficientes modificativos”, todos los coeficientes modificativos son menores que 1, donde mi nuevo Sn estará limitado por:
Sn=ka.kb.kc.kd.ke.kg.S`n                 (Ec. 3.4)
En donde:
Sn = Límite de fatiga conseguido ( Kg/cm2).
S´n = Límite de fatiga de la probeta.
ka = coeficiente modificativo de superficie.
kb = coeficiente modificativo de tamaño.
kc = coeficiente modificativo de confianza.
kd = coeficiente modificativo de temperatura.
ke = coeficiente modificativo por concentración de tensiones (no es el mismo que el coeficiente kt de concentración de tensiones).
Kf = coeficiente modificativo por efectos diversos.

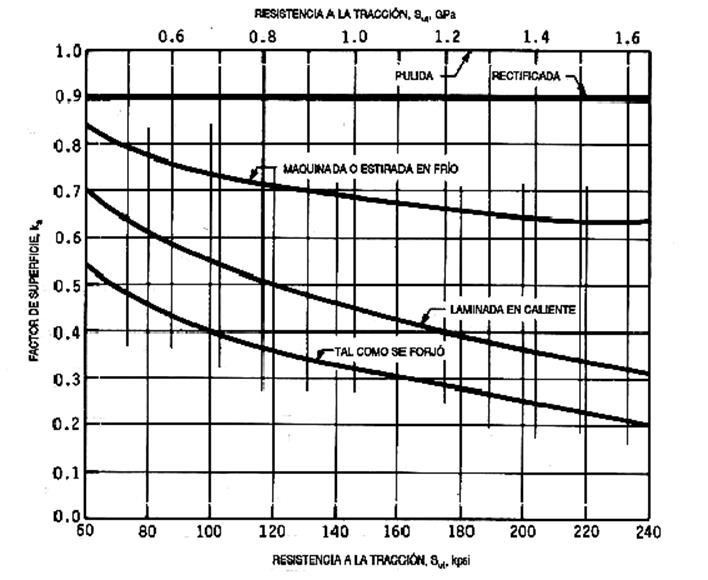
• ACABADO SUPERFICIAL (Ka): Tiene un efecto muy significativo sobre el límite de fatiga.

Tabla 3.1: Factor de Corrección Ka de acabado superficial

• EFECTOS DE TAMAÑO(Kb): El ensayo de la viga rotativa proporciona el límite de fatiga para una probeta de 0.3” Ø

Para probetas de mayor tamaño se ha encontrado que el límite de fatiga es de un 10 a 15% menor.

• Por tanto para flexión y torsión el coeficiente de tamaño es de kb=0.85.
• Para cargar axiales kb=1.

• COEFICIENTE DE CONFIANZA O SEGURIDAD FUNCIONAL(Kc):

Stilen, Cummings y Schulte; establecieron que la distribución de la relación de las resistencias a la fatiga era normal para un número fijo de ciclos.
Factor de confianza:
Kc = 1 - 0.08 D                 (Ec. 3.5)
Relación de supervivencia por 100        Factor de multiplicación de la desviación          D
          90                                                                           1.3
          95                                                                           1.6
          99                                                                           2.3
          99.9                                                                        3.1
          99.99                                                                      3.7

• EFECTOS DE TEMPERATURA(Kd) :

Piezas que trabajan a temperaturas elevadas pueden fallar por “Creep” o fluencia o por fatiga o por una combinación de ambas (o debido a una corrosión) conocido como termofluencia.
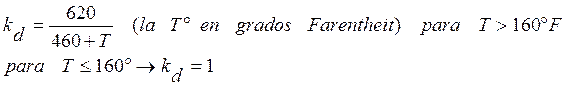(Ec. 3.6)

• SENSIBILIDAD A LA ENTALLA(Ke)

Un fallo por fatiga casi siempre se origina en una discontinuidad, la grieta empieza en una entalla, un resalte o en el borde de un orificio puede también iniciarse en una huella de herramienta o una raya.
Hay materiales que son mucho más sensibles a la entalla que otros.

• COEFICIENTE DE CONCENTRACIÓN DE TENSIONES EN LA FATIGA(Kf)

 

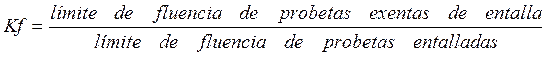 (Ec. 3.7)
El coeficiente modificativo de concentración de tensiones Ke está relacionado con Kf
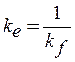                 (Ec. 3.8)
La sensibilidad a la entalla q:
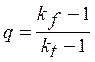              (Ec. 3.9)

Primero se halla Kt a partir de la geometría de la pieza, y luego el q:
               (Ec. 3.10)

• EFECTOS VARIOS(Kg)
• Tensiones residuales: Por tratamientos térmicos o trabaja en frío. si la tensión residual superficial es de compresión el límite de fatiga mejora (por ejemplo endurecimiento superficial mediante perdigones, el martillado y el laminado en frío).
• Características direccionales del material: Las piezas laminadas, forjadas o estiradas presentan un 10 a 20 % de reducción del límite de fatiga en dirección transversal (que a lo largo de la dirección longitudinal).
• Defectos internos: Inclusiones de escoria u óxidos, partículas extrañas.
• Cementado: Pueden fallar en la capa exterior o en el núcleo.
• Corrosión: Se debe al picado que produce la corrosión y el someter a la pieza a tensiones aumenta la corrosión.
• Metalizado: Como el cromado, niquelado y cadmiado reducen el límite de fatiga hasta en un 35%.

 

EjemploN°3.5:
El eje que se muestra a continuación tiene movimiento rotacional y está apoyado en cojinetes de bolas en A y D, los radios de empalme tienen 3 mm de radio y el acero es un AISI 1050 estirado en frío y tiene un acabado a máquina.
Se desea evaluar la duración de este elemento.

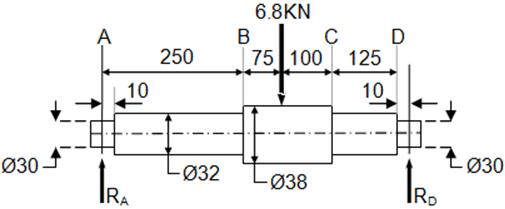
Características del material    Su = 690 Mpa
Sy = 580 Mpa

 

 

 

 

 

 

 

 

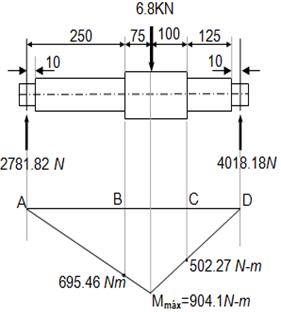
Solución:
RA+RD = 6800 N
RA . 550 – 68000 x 225 = 0
RA = 2781.82 N
RD = 4018.18 N

Resistencia a la fatiga: S’n = 0.5 x 690 = 345 MPa

Por tabla (3.1) el coeficiente de superficie para un Su = 690 MPa, es Ka=0.75

Coeficiente de tamaño Kb = 0.85 (para flexión y torsión)
Factor de concentración de esfuerzo
         
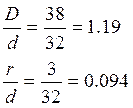
Sensibilidad a la entalla q = 0.84

 

 

 

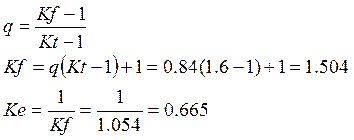
Por tanto el esfuerzo (de cálculo) para fatiga es:

El máximo esfuerzo está en el punto B (que es el que tiene mayor momento):
MB = 695.46 N.m.
El módulo de la sección: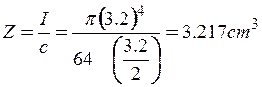

 

 

 

 

 

 

 

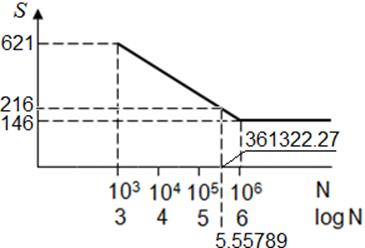
El esfuerzo en la sección B:

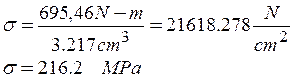
Este esfuerzo es mayor que el límite de fatiga  por lo tanto el elemento tiene una vida finita.

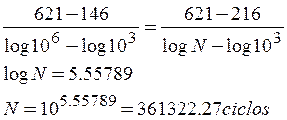
EjemploN°3.6:

 

 

 

 

 

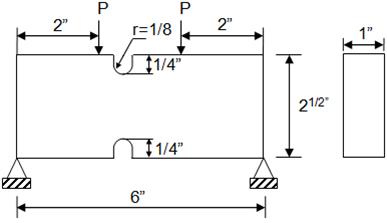
Imaginemos que la barra soporta tanto por la parte superior como por la parte inferior de tal manera que la carga P pueda ser invertida por completo.  Encuéntrese el valor numérico de la carga completamente invertida que someterá la barra en la muesca hasta el límite de duración.
Material SAE 1050:  Sy = 49,500 psi    Su = 90,000 psi
Solución: kt = 2.45 ; q = 0.9
Según gráfica: