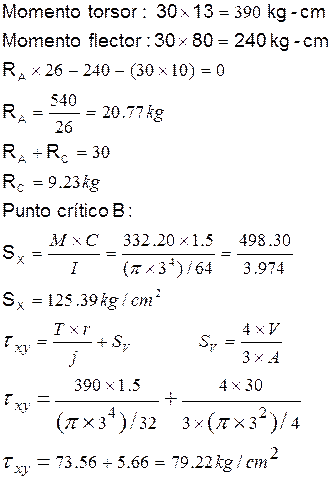2.3.-DIAGRAMA DEL CÍRCULO DE MOHR
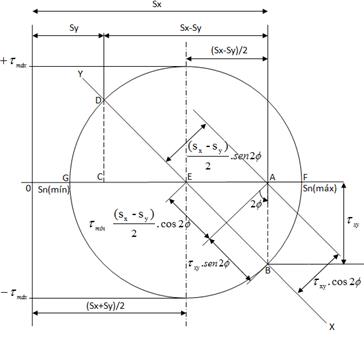
Método gráfico para expresar las relaciones obtenidas de los esfuerzos, muy eficaz para visualizar el estado de esfuerzos y tener en cuenta la dirección de un sistema de coordenadas.
- Los esfuerzos normales se representan en las abscisas y los cortantes en las ordenadas.
- Los esfuerzos principales también vienen dados por:
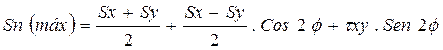( Ec. 2.13) 
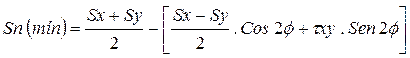(Ec. 2.14)
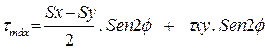(Ec. 2.15)
Fig.2.6
EjemploN°2.2:
Un elemento de esfuerzo tiene 
, se desea hallar:
- Los esfuerzos y las direcciones principales, e indicar en el elemento su orientación correcta (con respecto al sistema xy)
- Trazar otro elemento que muestre
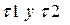determinando los esfuerzos normales correspondientes.
Gráficamente se pueden obtener los resultados
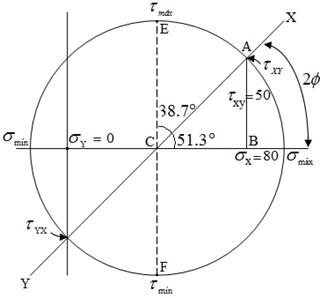
- Empleando las ecuaciones
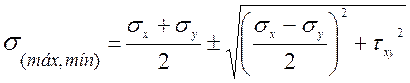
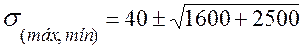
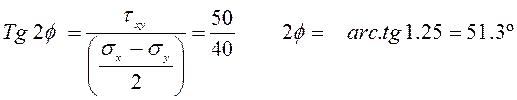
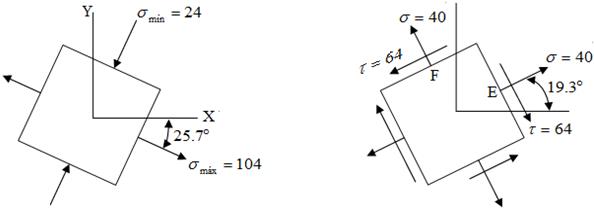
El esfuerzo esta a 45° respecto a las normales es decir 45°- 25.7°=19.3°
EjemploN°2.3:
- CARGA AXIAL
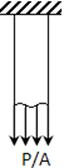
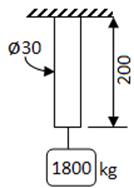
El elemento está sometido sólo a carga axial, se
desprecia el peso del elemento.
En cualquier parte del cuerpo estará sometido a un
mismo esfuerzo.
Área resistente: A = 900 mm2
Esfuerzo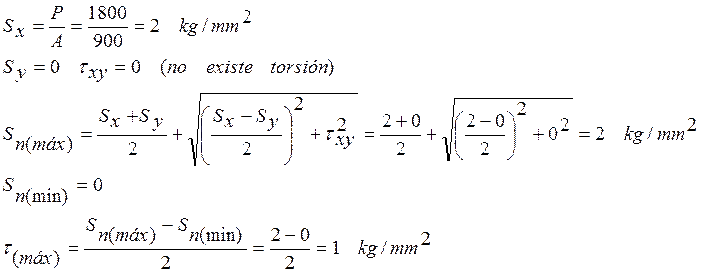
- FLEXIÓN
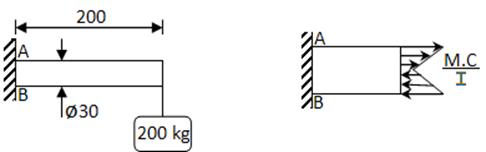
Los puntos A y B son críticos, porque soportan el mayor esfuerzo flector.
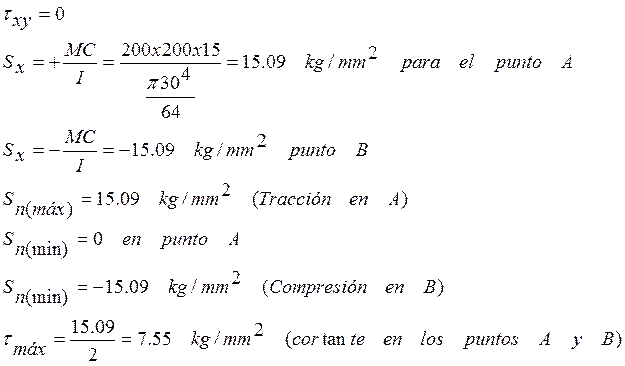
- TORSIÓN
Los puntos críticos se presentan a todo lo largo de la superficie exterior del elemento.
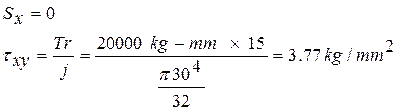
- CARGA AXIAL PURA
Si la barra es de sección cuadrada 4.5 cm de lado
En este caso todos los puntos del elemento están sometidos al mismo esfuerzo.
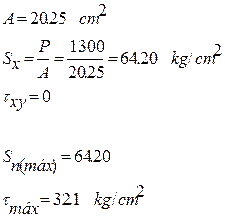
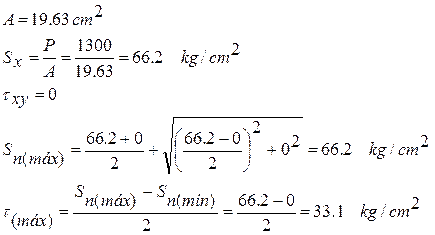
- FLEXIÓN AISLADA
Momento de inercia sección cuadrada
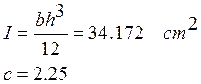
Los puntos A y B son puntos críticos
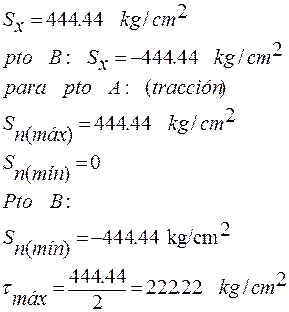
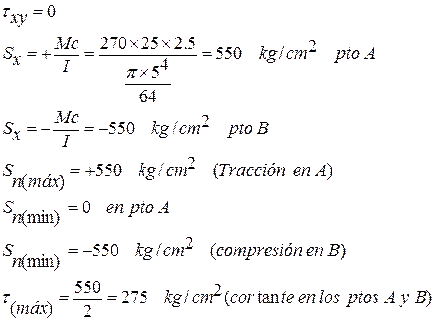
- TORSIÓN PURA
Los puntos críticos se presentan a todo lo largo de la superficie exterior del elemento.
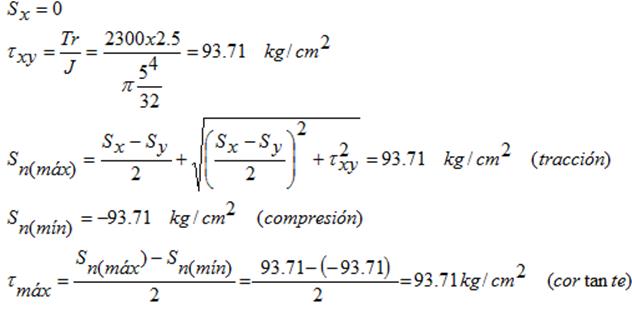
- FLEXIÓN Y TORSIÓN
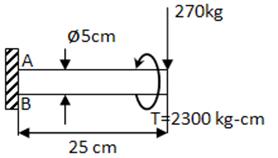
En el punto A:
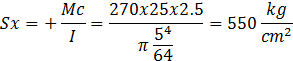
En el punto B:
Para el Punto A:
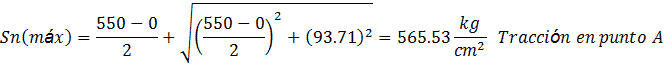
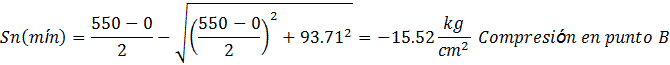
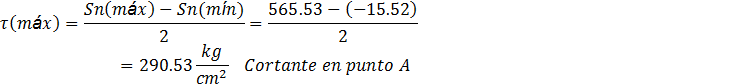
Para el Punto B
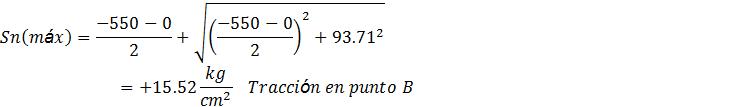
- Los signos de los esfuerzos normales máximos indican tracción o compresión, mientras que los signos de los esfuerzos cortantes máximos no tienen importancia ya que el diseño se basa en la magnitud.
- FLEXIÓN Y CARGA AXIAL
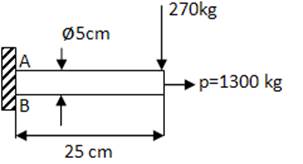
τxy = 0 no existe torsor
En el Punto A
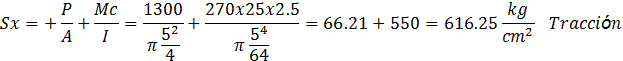
En el Punto B
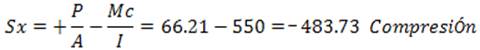
Otro ejemplo de flexión y carga axial:
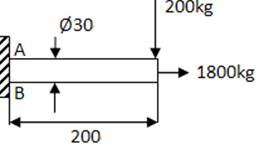
En el punto A
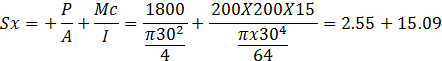
- TORSIÓN Y CARGA AXIAL
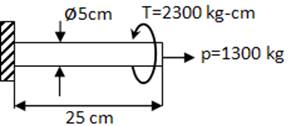
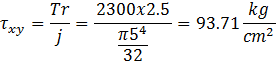
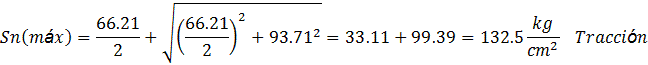
- FLEXIÓN, CARGA AXIAL Y TORSIÓN
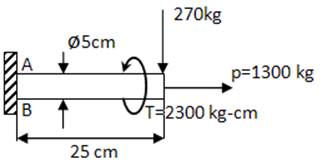
Los esfuerzos máximos se presentan en los puntos A y B.
En el punto A:
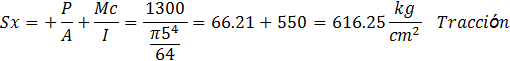
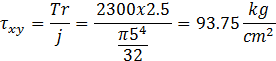
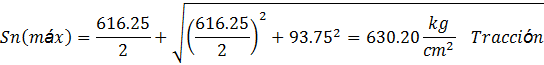
En el punto B:
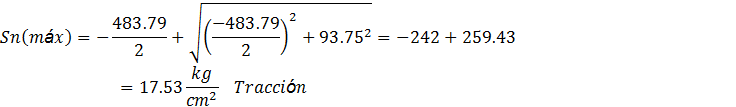
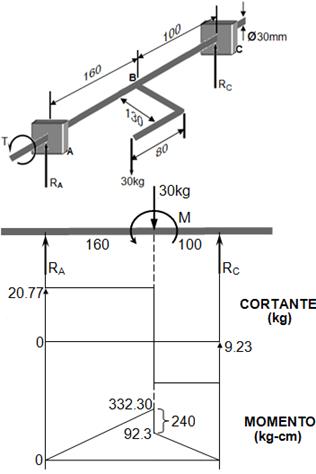
EjemploN°2.4: Calcular el esfuerzo cortante máximo en la sección A-A y en la sección B-B
Diagrama de cuerpo libre sobre la sección A-A
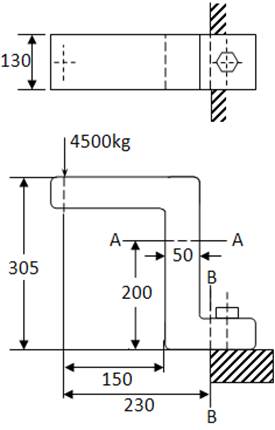
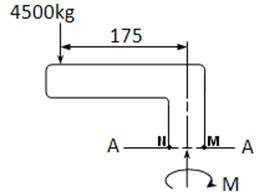
En el punto N, Sy=0 y Ƭxy=0
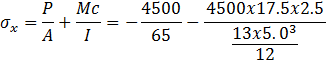
En la sección B-B
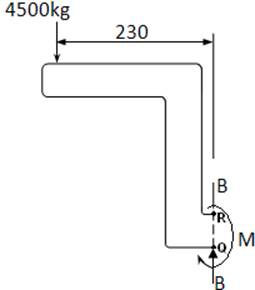
Diagrama de cuerpo libre
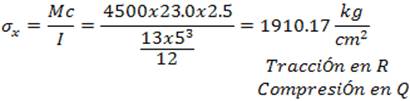
EjemploN°2.5: Determinar el esfuerzo normal máximo y el esfuerzo cortante máximo en la sección A-A
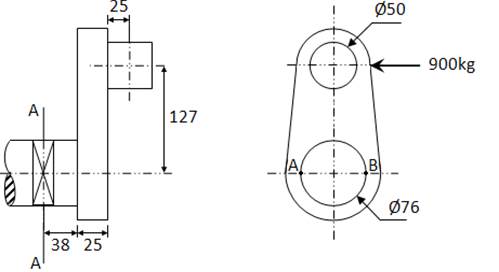
Puntos críticos en A y B
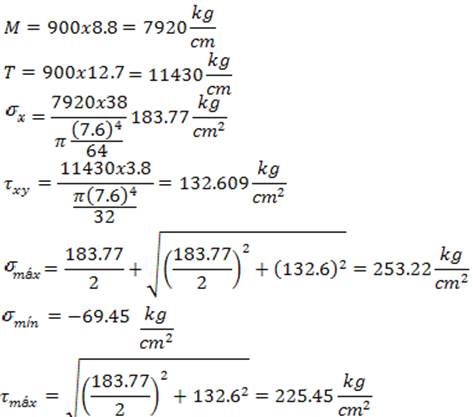
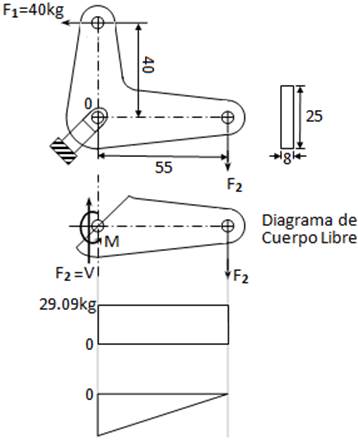
EjemploN°2.6:
El brazo que se muestra en la figura, es parte de un eslabón en que la fuerza horizontal de 40kg es transferida a F2 que actúa en forma vertical. La manivela puede pivotar sobre el pin 0.
Solución:
F2 x 5.5 = 40 x 4
F2 = 29.09 kg
La fuerza descendente F2 provoca un momento respecto a la sección del pin, existe un momento de reacción interna.
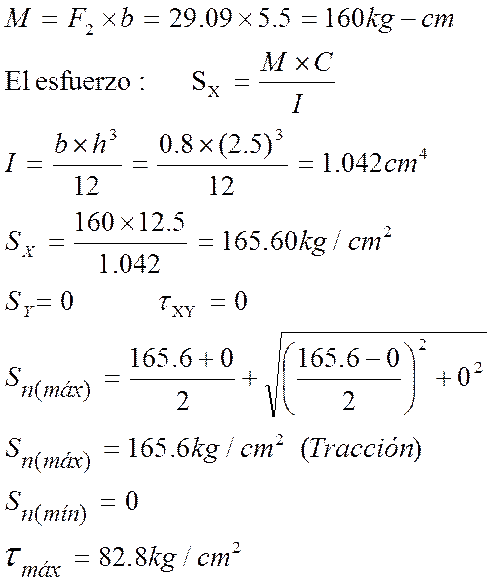
EjemploN°2.7:
Congresos
15 al 28 de febrero |
|
| Desafíos de las empresas del siglo XXI | |
15 al 29 de marzo |
|
| La Educación en el siglo XXI | |
Libro Gratis
 1647 - Investigaciones socioambientales, educativas y humanísticas para el medio rural Por: Miguel Ángel Sámano Rentería y Ramón Rivera Espinosa. (Coordinadores) Este libro es producto del trabajo desarrollado por un grupo interdisciplinario de investigadores integrantes del Instituto de Investigaciones Socioambientales, Educativas y Humanísticas para el Medio Rural (IISEHMER). Libro gratis |