3.4.-RESISTENCIA A LA FATIGA BAJO TENSIONES FLUCTUANTES
Hasta aquí solo hemos estudiado la manera de encontrar la magnitud de un esfuerzo completamente invertido que un material puede aguantar de manera indefinida. Esto lo representamos por la onda senoidal que se muestra en la Fig. 3.1b en la que el esfuerzo promedio ![]() =0. La mayor parte del tiempo, una situación de esfuerzo se asemeja a la que se describe en la Fig.3.1c en la que
=0. La mayor parte del tiempo, una situación de esfuerzo se asemeja a la que se describe en la Fig.3.1c en la que ![]() ≠0. Se emplean generalmente dos métodos:
≠0. Se emplean generalmente dos métodos:
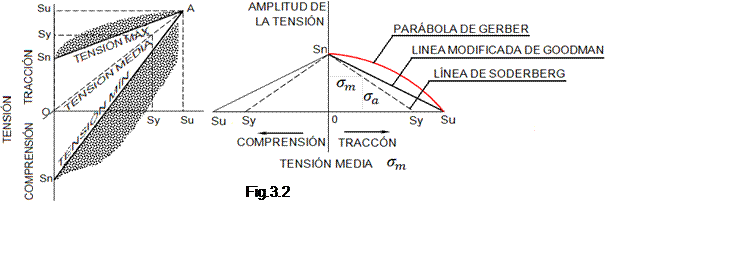
- Diagrama modificado de Goodman: Donde muestra todos los componentes.
- Cuando la tensión media es de compresión, el fallo se define por dos líneas paralelas gruesas
- Cuando la tensión media es de tracción al fallo se define por la tensión máxima o por el límite de fluencia.
Fig.3.3
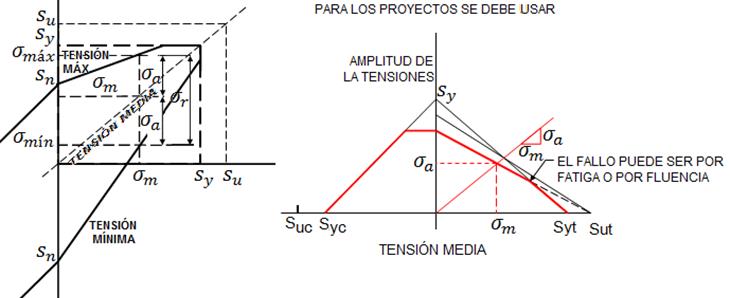
Esfuerzo que fluctúa para materiales dúctiles analizados por Gerber, Goodman y Soderberg:
Fig.3.4
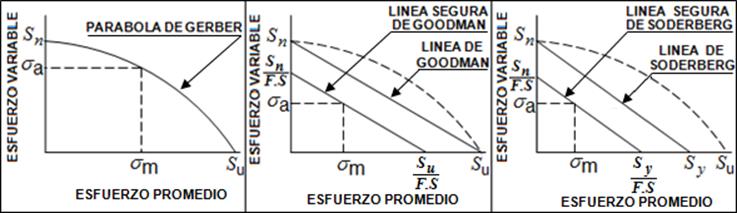
Si trazamos la componente del esfuerzo variable (
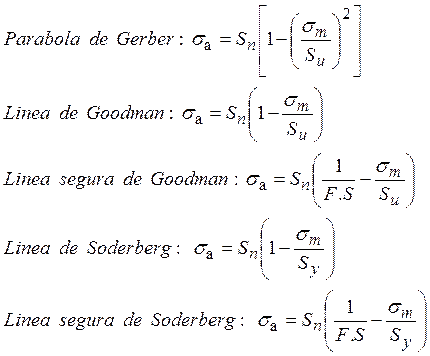
Ec. 3.14
Ec. 3.15
Ec. 3.16
Ec. 3.17
Ec. 3.18
A flexión completamente invertida el esfuerzo promedio es cero y el esfuerzo variable ![]() =Sn, lo que concuerda con la representación en la Fig. 3.1b y por otro lado, el esfuerzo promedio es la resistencia a la tensión,
=Sn, lo que concuerda con la representación en la Fig. 3.1b y por otro lado, el esfuerzo promedio es la resistencia a la tensión, ![]() =0 y tenemos la condición de un carga aplicada sólo una vez para originar la falla.
=0 y tenemos la condición de un carga aplicada sólo una vez para originar la falla.
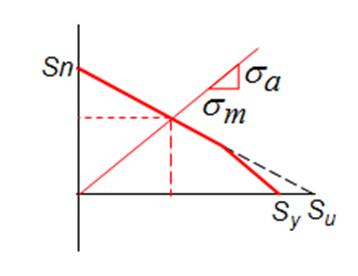
De las relaciones que obtuvimos podemos observar en la Fig.3.4 que la relación de Soderberg es más segura que la de Goodman y esta a su vez es más segura que la de Gerberg. En un sentido más conservador y para estar seguros de la certeza de los valores, en la línea de Goodman y de Soderber, tanto al Su como al Sy pueden dividirse por un factor arbitrario de seguridad (F.S), 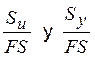 respectivamente con lo cual nos dará una relación más segura de la línea de Goodman y de Soderberg, obviamente el
respectivamente con lo cual nos dará una relación más segura de la línea de Goodman y de Soderberg, obviamente el ![]() calculado es menor que la relación sin el factor de seguridad.
calculado es menor que la relación sin el factor de seguridad.
EjemploN°3.7: Una parte de una máquina tiene un esfuerzo debido a flexión que fluctúa entre un esfuerzo de tensión de 40,000 lb/pulg2 y un esfuerzo de compresión de 20,000 lb/pulg2 ¿Cuál será la resistencia a la tensión mínima del acero que podría soportar estas fluctuaciones indefinidamente?
Aplique GERBER y GOODMAN
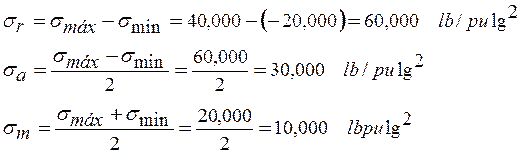
S’n=0.5 Su (para los aceros)
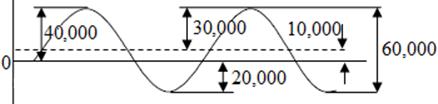
Según Gerber Según Goodman
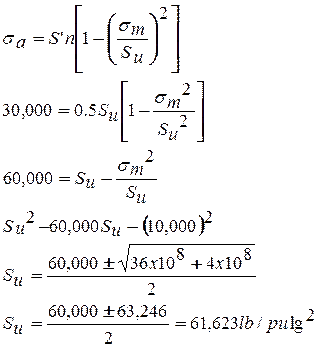
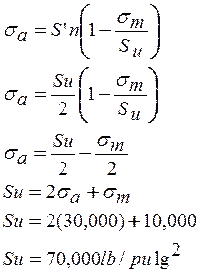
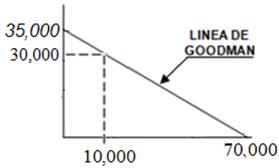
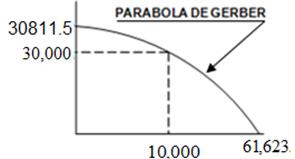
Aplicando Goodman con factor de seguridad 2:
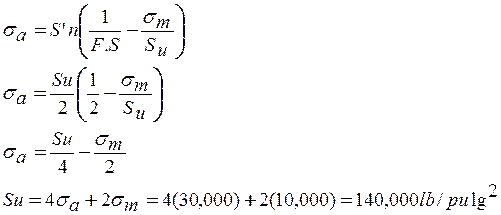
![]()
EjemploN°3.8: El mismo problema anterior, con un factor de seguridad 2 aplicando Soderberg. (Importante: Se sabe que Sy varía entre 0.55% - 0.95% de Su.)
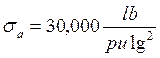
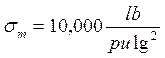
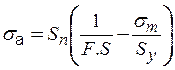
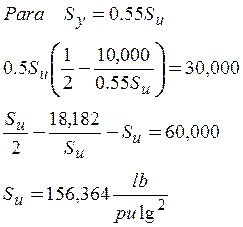
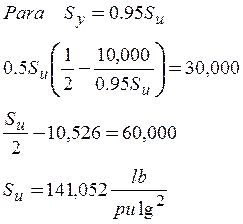
EjemploN°3.9: Una flecha de diámetro de 2” hecha de acero al carbono endurecida hasta 200 Brinell se sujeta a una torsión que fluctúa entre 24,000 lb–pulg y -6,000 lb-pulg ¿Cuál es el factor de seguridad por el método de Soderberg?
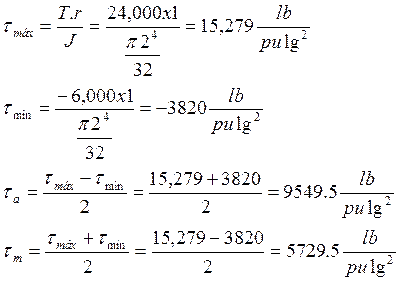
Importante: El límite de fatiga a torsión cíclica es aproximadamente la mitad del límite de duración a flexión.
- Para aceros:
![]()
![]()
- Para metales y aleaciones no ferrosas:
![]()
- Para fierro fundido:
![]()
- Por tablas: para acero al carbono de 200 Brinel:
Su = 100,000 psi
Sy = 55,000 psi
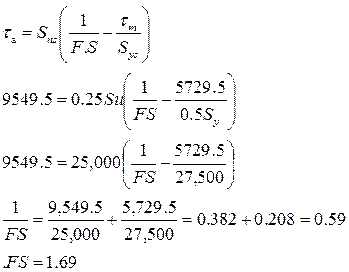
EjemploN°3.10: Una barra redonda de acero AISI C1018, estirada en frío, se proyecta para resistir una carga previa de tracción de 3600 kg y una carga fluctuante de tracción que varía de 0 a7200 kg. Debido al proyecto de sus extremos la barra tienen un coeficiente geométrico de concentración de tensiones de 2.10, que corresponde a un acuerdo de 3,20mm ¿Cuál será el radio de la barra, si el margen de seguridad nunca deberá ser menor de 100 por 100? La barra ha de proyectarse para una vida infinita.
SOLUCIÓN:
Según tablas el material tienen las siguientes propiedades mecánicas.
Sy = 4900 kg/cm2 Su = 5750 kg/cm2
Así pues el límite de fatiga será: S’n = 0.5xSu=2875 kg/cm2
El valor del coeficiente de superficie ka = 0.76
El valor del coeficiente de tamaño para cargas axiales kb = 1
El valor de la sensibilidad a la entalla q = 0.8
El valor de kf = 1+q(kt-1) = 1+0.8 (2.10 – 1) = 1.88
Dando como resultado el valor por concentración de tensiones
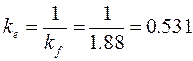
El valor del límite de fatiga será Sn = 1.76x1x0.531x2875=1,165 kg/cm2
Determinamos las tensiones:
- La tensión estática es:
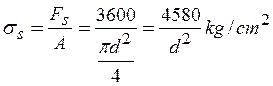
- Recorrido de las tensiones:
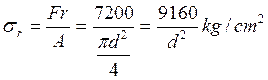
- Por tanto la amplitud:
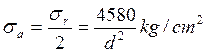
- En este caso la tensión media será:
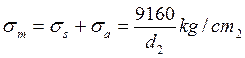
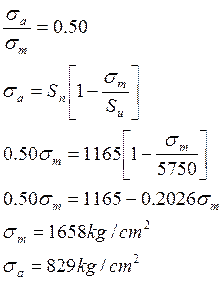
Como nos dice que debe tener una seguridad no menor de 100%: