Martín Carlos Ramales Osorio
Esta página muestra parte del texto pero sin formato.
Puede bajarse el libro completo en PDF comprimido ZIP (172 páginas, 1.33 Mb) pulsando aquí
LA FUNCIÓN DE CONSUMO Y LA DEMANDA AGREGADA
Una vez definido claramente el concepto de producción de equilibrio y cómo se determina, centremos la atención en los determinantes de la demanda agregada y, en particular, en la demanda de consumo. Para simplificar, omitimos tanto al Estado como al comercio exterior
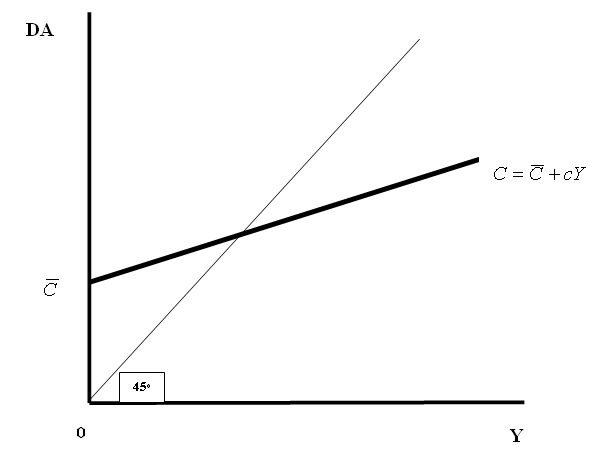
En la práctica la demanda de bienes de consumo no se mantiene constante, sino que aumenta conforme aumenta el nivel de la renta corriente (Y). La función de consumo describe la relación entre el consumo y la renta.
Suponemos que la demanda de consumo aumenta con el nivel de renta:
![]() (4)
(4)
Donde ![]() mayúscula del lado derecho es mayor a
cero
mayúscula del lado derecho es mayor a
cero ![]() y
y ![]() . Esta función de consumo se representa
en la Gráfica 4.2 por medio de la línea recta de tono más oscuro y grueso. La
variable
. Esta función de consumo se representa
en la Gráfica 4.2 por medio de la línea recta de tono más oscuro y grueso. La
variable ![]() , que es la ordenada en el origen,
representa el nivel de consumo cuando la renta corriente (Y) es cero, y recibe
por esa razón un nombre especial: consumo autónomo, es decir, es independiente
de la renta corriente (Y). Ese consumo autónomo depende del ahorro, de la venta
de activos o de los préstamos. Si en este momento no tengo una renta corriente
porque estoy desempleado de todos modos tengo que consumir algo, ¿de qué manera
puedo hacerlo? Pidiendo prestado a familiares o amigos, o al sistema financiero
bancario; si tengo algunos activos (como electrodomésticos, terrenos, joyas,
autos, etc.), vendiéndolos o empeñándolos; o si tengo algunos ahorros en el
banco, retirándolos para poder consumir.
, que es la ordenada en el origen,
representa el nivel de consumo cuando la renta corriente (Y) es cero, y recibe
por esa razón un nombre especial: consumo autónomo, es decir, es independiente
de la renta corriente (Y). Ese consumo autónomo depende del ahorro, de la venta
de activos o de los préstamos. Si en este momento no tengo una renta corriente
porque estoy desempleado de todos modos tengo que consumir algo, ¿de qué manera
puedo hacerlo? Pidiendo prestado a familiares o amigos, o al sistema financiero
bancario; si tengo algunos activos (como electrodomésticos, terrenos, joyas,
autos, etc.), vendiéndolos o empeñándolos; o si tengo algunos ahorros en el
banco, retirándolos para poder consumir.
Adicionalmente, en la ecuación (4) tenemos que otra parte del consumo depende de la renta corriente (Y) en una proporción c. Esta c minúscula se denomina “propensión marginal a consumir”, y se define de la siguiente manera;
- La propensión marginal a consumir es el aumento que experimenta el consumo por cada aumento unitario de la renta; y toma valores entre cero y uno: es mayor a cero, porque una parte por lo menos mínima se gasta en consumo; y es menor a uno, porque una fracción por lo menos mínima del aumento de la renta corriente de la colectividad se ahorra.
El nivel de consumo aumenta en c pesos por cada peso en que aumenta la renta corriente (Y) de la colectividad. Por ejemplo, si c es igual a 0.90, el consumo aumenta en 90 centavos por cada peso en que aumenta la renta. La pendiente de la función consumo es c. A lo largo de esta función, el nivel de consumo aumenta con la renta en una proporción c.
¿Qué ocurre con el resto del aumento de un peso de la renta corriente, es decir, con la proporción 1-c que no se gasta en consumo? Si no se gasta en consumo, debe ahorrarse. La renta corriente o se gasta o se ahorra; no puede utilizarse para otros fines.
En términos más formales, examinemos la ecuación 5 que establece que la renta que no se gasta en consumo se ahorra:
![]() (5)
(5)
Donde S es el ahorro, Y es la renta o el ingreso corriente, y C es el gasto en consumo. La ecuación (5) establece que por definición el ahorro (S) es igual a la renta corriente (Y) menos el consumo (C).
Gráfica 4.2: Representación geométrica de la función consumo
La función de consumo de la ecuación (4) junto con la (5), que denominamos restricción presupuestaria, implica una función de ahorro. La función de ahorro relaciona el nivel de ahorro y el nivel de renta. Introduciendo la función de consumo de la ecuación (4) en la restricción presupuestaria de la ecuación (5), tenemos la función de ahorro:
![]() (6)
(6)
Pero como ![]()
![]() (6a)
(6a)
U
ordenando: ![]()
Vemos en la
ecuación (6) que el ahorro es una función creciente del nivel de renta, ya que
la propensión marginal a ahorrar, ![]() , es positiva. En otras palabras, el
ahorro aumenta cuando aumenta la renta. Supongamos, por ejemplo, que la
propensión marginal a consumir, c, es 0.90, lo que significa que se
consumen 90 centavos de cada peso adicional de renta. En ese caso, la propensión
marginal a ahorrar, s, es 0.10, lo que significa que los 10 centavos
restantes de cada peso adicional de renta se ahorran.
, es positiva. En otras palabras, el
ahorro aumenta cuando aumenta la renta. Supongamos, por ejemplo, que la
propensión marginal a consumir, c, es 0.90, lo que significa que se
consumen 90 centavos de cada peso adicional de renta. En ese caso, la propensión
marginal a ahorrar, s, es 0.10, lo que significa que los 10 centavos
restantes de cada peso adicional de renta se ahorran.
De manera más
intuitiva, llegamos a (6a) considerando que si se gastan 90 centavos de cada
peso adicional de renta corriente, entonces 10 centavos se deben estar ahorrando
por parte de la colectividad, de manera tal que multiplicamos el valor de la
propensión marginal a ahorrar (0.10) por la renta corriente total y obtenemos el
ahorro total de la economía, al que debemos restarle el consumo autónomo ![]() nada más, porque el consumo que depende
de la renta corriente total (Y) ya está descontado, por así decirlo, en el
cálculo de sY.
nada más, porque el consumo que depende
de la renta corriente total (Y) ya está descontado, por así decirlo, en el
cálculo de sY.
LA INVERSIÓN PLANEADA Y LA DEMANDA AGREGADA
Hemos
especificado uno de los componentes de la demanda agregada; a saber, la demanda
de consumo. También debemos considerar los determinantes del gasto en inversión,
o sea, una función de inversión. De momento, simplificamos el análisis
suponiendo simplemente que el gasto en inversión planeada se mantiene constante
en el nivel ![]() .
.
Al suponer que el gasto público y las exportaciones netas son iguales a cero, la demanda agregada es la suma de las demandas de consumo y de inversión:
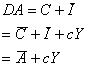 (7)
(7)
Donde.![]() es la demanda agregada autónoma, porque
se supone que es la suma del consumo autónomo
es la demanda agregada autónoma, porque
se supone que es la suma del consumo autónomo ![]() y de la inversión autónoma
y de la inversión autónoma ![]() ; inversión autónoma
; inversión autónoma ![]() porque se supone que es independiente de
la renta corriente (Y) y de la tasa de interés (i), supuesto que en la práctica
se desvanece. La Gráfica 4.3 representa la función de demanda agregada (DA) dada
por (7). Para obtener la curva de demanda agregada (DA), a la función consumo le
sumamos verticalmente la demanda de inversión que suponemos de momento es
autónoma. Una parte de la demanda agregada
porque se supone que es independiente de
la renta corriente (Y) y de la tasa de interés (i), supuesto que en la práctica
se desvanece. La Gráfica 4.3 representa la función de demanda agregada (DA) dada
por (7). Para obtener la curva de demanda agregada (DA), a la función consumo le
sumamos verticalmente la demanda de inversión que suponemos de momento es
autónoma. Una parte de la demanda agregada![]() es independiente del nivel de renta, es
decir, es autónoma. Pero la demanda agregada también depende del nivel de renta.
Aumenta con el nivel de renta porque la demanda de consumo aumenta con la renta.
La curva de demanda agregada (DA), repetimos, se obtiene sumando (verticalmente)
las demandas de consumo y de inversión correspondientes a cada nivel de renta.
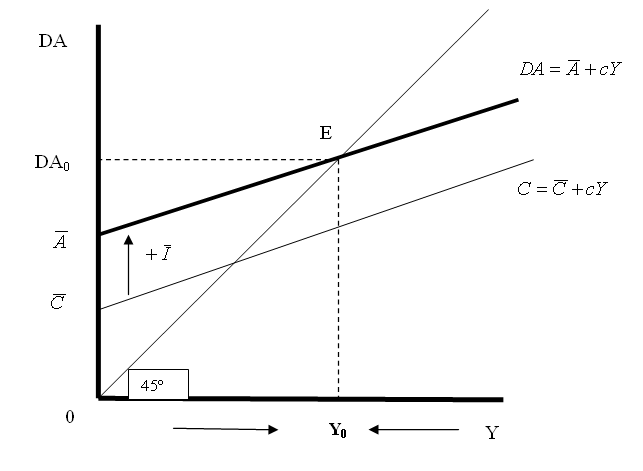
En el nivel de renta Y0 de la Gráfica 4.3, el nivel de demanda
agregada es DA0.
es independiente del nivel de renta, es
decir, es autónoma. Pero la demanda agregada también depende del nivel de renta.
Aumenta con el nivel de renta porque la demanda de consumo aumenta con la renta.
La curva de demanda agregada (DA), repetimos, se obtiene sumando (verticalmente)
las demandas de consumo y de inversión correspondientes a cada nivel de renta.
En el nivel de renta Y0 de la Gráfica 4.3, el nivel de demanda
agregada es DA0.
La producción se encuentra en su nivel de equilibrio cuando la demanda agregada (DA) es igual a la producción (Y); es decir, en el punto E que corresponde al nivel de producción (y de renta) Y0. En cualquier nivel de producción más alto, la demanda agregada es inferior al nivel de producción, las empresas no pueden vender todo lo que producen y hay una acumulación involuntaria de existencias (IU). Por lo tanto, las empresas reducen la producción, como muestran las flechas de la Gráfica 4.3 que se muestra enseguida. Asimismo, en cualquier nivel de producción inferior a Y0, la demanda agregada es superior a la producción, las empresas se quedan sin bienes para vender, por lo que tienen que aumentar la producción. Las empresas sólo producen la cantidad que se demanda.
Gráfica 4.3: La función consumo y la curva de demanda agregada (DA)
Entonces, tenemos que en el equilibrio la producción (Y) es exactamente igual a la demanda agregada (DA):
![]()
Pero como
![]()
Entonces es mejor escribir:
![]() (8)
(8)
Dado que Y aparece en los dos miembros de la condición de equilibrio de la ecuación (8), podemos agrupar términos y despejar el nivel de renta o producción de equilibrio, representado por Y0:
![]() (9)
(9)
Tenemos
entonces en (9) que la renta de equilibrio, Y0, es un múltiplo de la
demanda agregada autónoma, ![]() , porque
, porque ![]() es el llamado multiplicador del gasto,
en donde c es la propensión marginal a consumir. Entonces el valor del
multiplicador depende del valor de c: mientras mayor sea el valor de c
mayor será el valor del multiplicador, y viceversa. Por ejemplo, si el valor de
c es de 0.70 el valor del multiplicador será de 3.33
es el llamado multiplicador del gasto,
en donde c es la propensión marginal a consumir. Entonces el valor del
multiplicador depende del valor de c: mientras mayor sea el valor de c
mayor será el valor del multiplicador, y viceversa. Por ejemplo, si el valor de
c es de 0.70 el valor del multiplicador será de 3.33 ![]() , en cambio si c fuera de 0.85 el valor
del multiplicador sería de 6.67
, en cambio si c fuera de 0.85 el valor
del multiplicador sería de 6.67 ![]() . En el primer caso, por cada peso en
que aumente el consumo o la inversión autónoma la producción o la renta de
equilibrio aumentará en 3 pesos con 33 centavos; y en el segundo caso, por cada
peso de aumento en la demanda agregada autónoma la renta de equilibrio aumentará
en 6 pesos con 67 centavos. ¿Cómo se puede explicar intuitivamente esto del
multiplicador? Considere la construcción de una carretera por parte del
gobierno, entre otras muchas cosas se requiere mano de obra. Si la carretera va
a pasar por la ciudad de Huajuapan, se demandará mano de obra del lugar y
también de otras partes. A su vez los trabajadores requerirán de ciertos
servicios, sobre todo los foráneos: comida, lavado de ropa, vivienda, etc. Las
personas que venden comidas verán incrementadas sus ventas, lo que hará que
elaboren más comidas, y para elaborar más comidas se requieren de más insumos
(verduras, legumbres, etc.) y más mano de obra. Esto estimula a los agricultores
a incrementar su producción de legumbres, verduras, frutas, etc., pero para que
puedan hacerlo requieren, a su vez, de más semilla, fertilizantes, mano de obra
etc. Es decir, la economía se ve sumergida en una serie de cadenas que llevan
finalmente a un incremento de la producción todavía mayor al incremento inicial
de la demanda. No obstante, la magnitud del incremento de la demanda dependerá
del valor de la propensión marginal a consumir.
. En el primer caso, por cada peso en
que aumente el consumo o la inversión autónoma la producción o la renta de
equilibrio aumentará en 3 pesos con 33 centavos; y en el segundo caso, por cada
peso de aumento en la demanda agregada autónoma la renta de equilibrio aumentará
en 6 pesos con 67 centavos. ¿Cómo se puede explicar intuitivamente esto del
multiplicador? Considere la construcción de una carretera por parte del
gobierno, entre otras muchas cosas se requiere mano de obra. Si la carretera va
a pasar por la ciudad de Huajuapan, se demandará mano de obra del lugar y
también de otras partes. A su vez los trabajadores requerirán de ciertos
servicios, sobre todo los foráneos: comida, lavado de ropa, vivienda, etc. Las
personas que venden comidas verán incrementadas sus ventas, lo que hará que
elaboren más comidas, y para elaborar más comidas se requieren de más insumos
(verduras, legumbres, etc.) y más mano de obra. Esto estimula a los agricultores
a incrementar su producción de legumbres, verduras, frutas, etc., pero para que
puedan hacerlo requieren, a su vez, de más semilla, fertilizantes, mano de obra
etc. Es decir, la economía se ve sumergida en una serie de cadenas que llevan
finalmente a un incremento de la producción todavía mayor al incremento inicial
de la demanda. No obstante, la magnitud del incremento de la demanda dependerá
del valor de la propensión marginal a consumir.
Cuando aumenta la demanda
agregada autónoma ![]() , la curva de demanda agregada se
desplaza en sentido ascendente a DA´. El equilibrio se desplaza de E a E´. El
aumento de la producción de equilibrio (Y1 – Y0), que es
igual a la distancia representada por la flecha horizontal bidireccional, es
superior al incremento del gasto autónomo, representado a su vez por la
distancia dada por las flechas verticales bidireccionales (Ver Gráfica 4.4).
Vemos en la Gráfica 4.4 que es mayor porque la curva de demanda agregada tiene
pendiente positiva en lugar de ser horizontal. En otras palabras, el
multiplicador es superior a 1 porque la demanda de consumo aumenta con la renta:
cualquier aumento de la producción provoca nuevos aumentos de la demanda. Si
c es 0.8 el valor del multiplicador será de 5, de manera tal que si el gasto
autónomo aumenta en un peso la renta de equilibrio aumentará en 5 pesos.
, la curva de demanda agregada se
desplaza en sentido ascendente a DA´. El equilibrio se desplaza de E a E´. El
aumento de la producción de equilibrio (Y1 – Y0), que es
igual a la distancia representada por la flecha horizontal bidireccional, es
superior al incremento del gasto autónomo, representado a su vez por la
distancia dada por las flechas verticales bidireccionales (Ver Gráfica 4.4).
Vemos en la Gráfica 4.4 que es mayor porque la curva de demanda agregada tiene
pendiente positiva en lugar de ser horizontal. En otras palabras, el
multiplicador es superior a 1 porque la demanda de consumo aumenta con la renta:
cualquier aumento de la producción provoca nuevos aumentos de la demanda. Si
c es 0.8 el valor del multiplicador será de 5, de manera tal que si el gasto
autónomo aumenta en un peso la renta de equilibrio aumentará en 5 pesos.
Gráfica
4.4: El efecto multiplicador de un aumento de la demanda agregada autónoma ![]() sobre la producción o renta de
equilibrio (Y)
sobre la producción o renta de
equilibrio (Y)
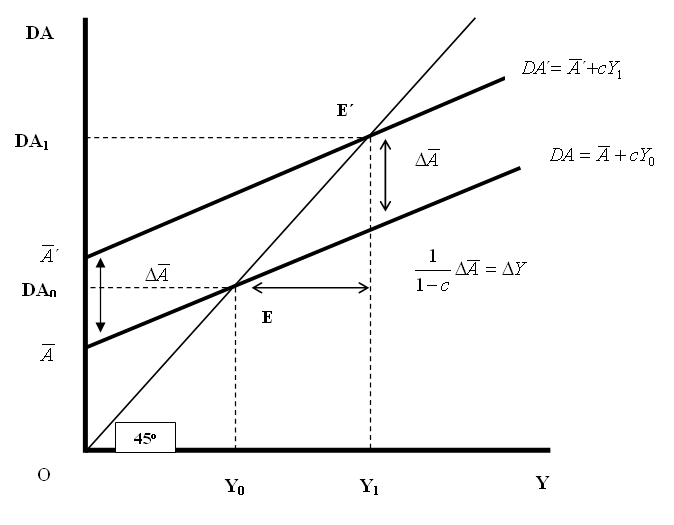
Cabe señalar que en el
equilibrio del mercado de productos (que por el momento representamos con la
recta de 45º y la curva de demanda agregada), no sólo la producción (Y) es igual
a la demanda agregada (DA) sino que también se cumple la condición de que el
ahorro (S) es siempre igual a la inversión ![]() . Con las ecuaciones obtenidas
anteriormente, resolvamos el siguiente ejercicio (más adelante resolveremos el
mismo sistema aquí presentado por álgebra de matrices, en particular por regla
de Cramer):
. Con las ecuaciones obtenidas
anteriormente, resolvamos el siguiente ejercicio (más adelante resolveremos el
mismo sistema aquí presentado por álgebra de matrices, en particular por regla
de Cramer):
EJERCICIO 1:
Suponga una economía hipotética descrita por las siguientes funciones: ![]() e
e ![]() : a) obtenga el valor del multiplicador,
b) ¿cuál es el nivel de la demanda agregada autónoma
: a) obtenga el valor del multiplicador,
b) ¿cuál es el nivel de la demanda agregada autónoma ![]() ?, c) ¿cuál es el nivel de la renta o
producción de equilibrio (Y)?, d) verifique que en el equilibrio el ahorro (S)
es igual a la inversión
?, c) ¿cuál es el nivel de la renta o
producción de equilibrio (Y)?, d) verifique que en el equilibrio el ahorro (S)
es igual a la inversión ![]() , e) grafique la renta o producción de
equilibrio de este modelo, f) ahora suponga que
, e) grafique la renta o producción de
equilibrio de este modelo, f) ahora suponga que ![]() aumenta a 962, ¿qué ocurre con el valor
de la demanda agregada autónoma
aumenta a 962, ¿qué ocurre con el valor
de la demanda agregada autónoma ![]() y, por tanto, con el nivel de la renta
de equilibrio?, g) represente gráficamente este cambio experimentado por la
demanda agregada autónoma
y, por tanto, con el nivel de la renta
de equilibrio?, g) represente gráficamente este cambio experimentado por la
demanda agregada autónoma ![]() , h) vuelva a verificar que en el
equilibrio el ahorro es igual a la inversión.
, h) vuelva a verificar que en el
equilibrio el ahorro es igual a la inversión.
SOLUCIÓN:
a) De la ecuación (9) tenemos que el multiplicador (M) es: ![]() ; por tanto, con los datos que tenemos
M es igual a:
; por tanto, con los datos que tenemos
M es igual a: ![]() .
.
b) La demanda agregada autónoma es ![]() ; por tanto, con los datos que tenemos
; por tanto, con los datos que tenemos
![]() asciende a:
asciende a: ![]() .
.
c) Utilizando la ecuación (9) obtenida más arriba, la renta de equilibrio
es: ![]() .
.
d) Para obtener el ahorro podemos utilizar la ecuación (5), S = Y – C; o
bien, la ecuación (6a), ![]() . Utilicemos primero la ecuación 5; no
obstante, obtengamos primero el valor del consumo, el valor de la renta ya lo
tenemos y es de 5930.8404. ¿Cómo obtenemos el valor del consumo? Utilizando la
función dada al principio del ejercicio: C = 683 + 0.74 (5930.8404) = 683 +
4388.8219 = 5071.8219. Por lo que el ahorro asciende a:
. Utilicemos primero la ecuación 5; no
obstante, obtengamos primero el valor del consumo, el valor de la renta ya lo
tenemos y es de 5930.8404. ¿Cómo obtenemos el valor del consumo? Utilizando la
función dada al principio del ejercicio: C = 683 + 0.74 (5930.8404) = 683 +
4388.8219 = 5071.8219. Por lo que el ahorro asciende a:
S = 5930.8404 – 5071.8219 = 859.02.
Que es, en efecto, igual al
valor de la inversión autónoma ![]() arrojado al principio del enunciado del
ejercicio: 859.
arrojado al principio del enunciado del
ejercicio: 859.
Ahora utilicemos la
ecuación (6a) para obtener el ahorro: ![]() . El valor del consumo autónomo
. El valor del consumo autónomo ![]() es de 683, el valor de la renta de
equilibrio de 5930.8404, y el valor de s, que recibe la denominación de
propensión marginal a ahorrar, se obtiene de la siguiente manera: s = 1 – c;
por tanto, despejando datos: s = 1 – 0.74 = 0.26. Estamos en condición,
pues, de utilizar (6a):
es de 683, el valor de la renta de
equilibrio de 5930.8404, y el valor de s, que recibe la denominación de
propensión marginal a ahorrar, se obtiene de la siguiente manera: s = 1 – c;
por tanto, despejando datos: s = 1 – 0.74 = 0.26. Estamos en condición,
pues, de utilizar (6a):
S = -683 + 0.26 (5930.8404) = -683 + 1542.0185 = 859.02.
e) La gráfica es como sigue:
Gráfica 4.5: Efecto de un aumento de la inversión autónoma sobre la producción o renta de equilibrio (Y)
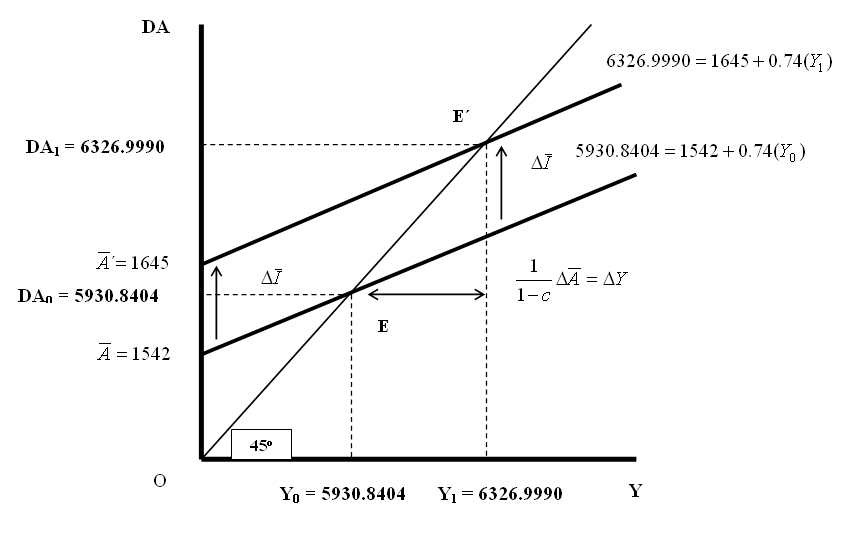
f) Si la inversión autónoma ![]() aumenta de 859 a 962, entonces la
demanda agregada autónoma
aumenta de 859 a 962, entonces la
demanda agregada autónoma ![]() es igual a:
es igual a: ![]() ; en consecuencia, la renta o producción
de equilibrio (Y) se incrementa a:
; en consecuencia, la renta o producción
de equilibrio (Y) se incrementa a:
Y = 3.8462 (1645) = 6326.9990
O sea, que la producción o renta de equilibrio aumentó en 396.1586 al haber pasado de 5930.8404 a 6326.9990; o una tasa de crecimiento del 6.68 por ciento.
g) El cambio experimentado en la inversión autónoma ![]() y, por tanto, en la demanda agregada
autónoma
y, por tanto, en la demanda agregada
autónoma ![]() se representa en la gráfica del inciso
e.
se representa en la gráfica del inciso
e.
h) Verifiquemos nuevamente que en el equilibrio el ahorro es igual a la inversión (962), utilizando (5). Pero obtengamos primero el valor del consumo: C = 683 + 0.74 (6326.9990) = 683 + 4681.9793 = 5364.9793.
Por tanto el ahorro es: S = 6326.9990 – 5364.9793 = 962.02. Tal como lo esperábamos.
El anterior es el
planteamiento que hacen Dornbusch y Fischer en la tercera edición de su libro de
macroeconomía. Planteamiento que se puede resolver por regla de Cramer. Tenemos
que la renta o producción de equilibrio (Y) es igual al consumo (C) más la
inversión autónoma ![]() , y la función consumo es como antes:
, y la función consumo es como antes:
![]()
![]()
![]()
Mismas que pueden disponerse de la siguiente forma:
![]()
![]()
Donde las variables
endógenas Y y C aparecen sólo en el lado izquierdo de las igualdades, mientras
que las variables exógenas ![]() y los parámetros aislados aparecen
sólo en el lado derecho. La matriz de coeficientes es:
y los parámetros aislados aparecen
sólo en el lado derecho. La matriz de coeficientes es:
![]()
![]() Y
el vector columna de constantes (datos) es:
Y
el vector columna de constantes (datos) es:
![]()
![]()
La regla de Cramer nos lleva a la siguiente solución:
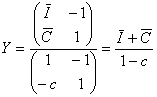
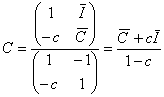
Por tanto, resolvamos ahora el ejercicio 1 utilizando las ecuaciones obtenidas de esta manera:
a) La renta de equilibrio es:
![]()
Que por centésimas difiere
de la renta obtenida más arriba. Aquí el valor del multiplicador lo obtendríamos
dividiendo la renta o producción de equilibrio (Y) entre el valor de la demanda
agregada autónoma ![]() :
:
![]()
b) La demanda agregada
autónoma ![]() la hemos obtenido en el numerador de la
ecuación de la renta de equilibrio, y es 1542 (= 859 + 683), igual que el valor
obtenido más arriba.
la hemos obtenido en el numerador de la
ecuación de la renta de equilibrio, y es 1542 (= 859 + 683), igual que el valor
obtenido más arriba.
c) Ahora verifiquemos que el ahorro es igual a la inversión. Ya tenemos el valor de la renta que es de 5930.7692, calculemos el valor del consumo para después proceder a la obtención del ahorro. El consumo lo calculamos con la segunda ecuación obtenida por regla de Cramer que es:
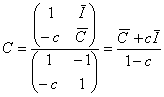
![]()
Por lo que el ahorro es:
![]()
Que es exactamente igual al
valor de la inversión autónoma arrojado a principios del enunciado del ejercicio
1: ![]() .
.
d) Ahora veamos qué ocurre con el valor de la demanda agregada autónoma
![]() , y por tanto, con el nivel de la renta
de equilibrio (Y) cuando
, y por tanto, con el nivel de la renta
de equilibrio (Y) cuando ![]() aumenta a 962.
aumenta a 962.
Tenemos lo siguiente:
![]()
Por lo que la renta
de equilibrio se incrementa a: ![]()
Que es un resultado muy similar al obtenido en el inciso f.
e) Volvamos a verificar que el ahorro (S) es igual al valor de la inversión
![]() , que ahora es de 962.
, que ahora es de 962.
Utilizando la ecuación para el consumo obtenida por regla de Cramer tenemos:
![]()
Por lo que el ahorro es
igual a: ![]()
Que es exactamente igual al valor de la inversión.
En consecuencia, cuando aumenta el consumo autónomo o la inversión autónoma, o ambos, aumenta la demanda agregada autónoma y, vía el multiplicador, aumenta la producción o renta de equilibrio; y viceversa. Gráficamente esto se representa mediante un desplazamiento paralelo de la curva de demanda agregada hacia arriba y a la izquierda, tal como se representa en la gráfica del inciso e.
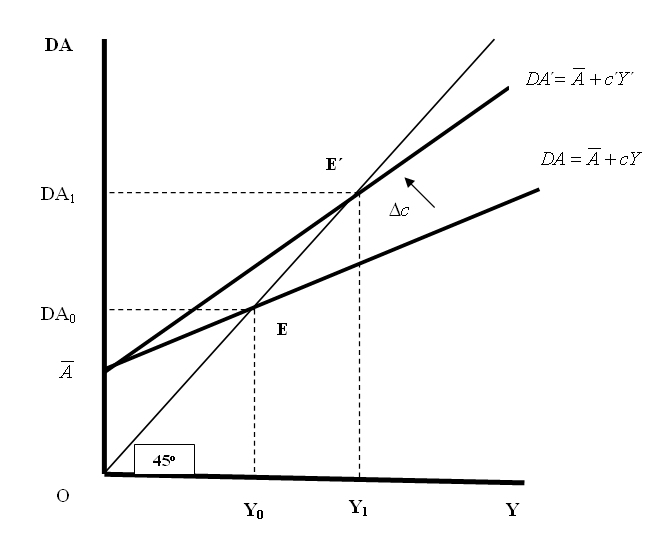
En cambio, cuando aumenta el valor de la propensión marginal a consumir, c, aumenta el valor del multiplicador y, por tanto, el nivel de la renta de equilibrio; y viceversa. Cambio que se representa gráficamente “rotando” la curva de demanda agregada en sentido inverso al de las manecillas del reloj, tal como lo hacemos en la siguiente gráfica:
Gráfica 4.6: Efecto sobre la producción o renta de equilibrio (Y) de un aumento de la propensión marginal a consumir, c.