INTRODUCCIÓN
“Marx estaba en lo cierto” quizá sea una expresión que no contente a algunos, sin embargo los hechos recientes que se vienen dando en la economía mundial dan para decir esto y muchas cosas más. Esta afirmación 1 es sostenida en base al estudio del Ejército Industrial de Reserva y la comprensión de su lógica al influir en la participación de los trabajadores en la renta nacional.
La dinámica del Ejército Industrial de Reserva y su influencia en la participación de los trabajadores en la producción posee una formalización bastante interesante que es el trabajo desarrollado por Richard Goodwin (1967) en el cual plantea que la economía no se encuentra en un punto de equilibrio único sino que se mantiene en constante fluctuación, lo cual es una alternativa muy llamativa respecto a los modelos tradicionales que buscan explicar la dinámica de los ciclos económicos y el comportamiento de la economía a largo plazo como el caso de Solow (1956).
Si bien la literatura existente sobre el modelo de Goodwin es accesible y existen aplicaciones empíricas recientes relacionadas a este modelo 2 sin embargo el modelo mencionado posee bastantes potencialidades que podrían ser desarrolladas con el fin de comprender más profundamente la dinámica del Ejército Industrial de Reserva.
En este sentido, las breves líneas aquí escritas solo plantearán una de esas potencialidades, la cual tiene que ver con la dinámica existente entre el Ejército Industrial de Reserva y la tasa de explotación manteniendo, dentro de lo posible, “intactos” los aspectos fundamentales y la metodología aplicada en el modelo de Goodwin.
MODELO DE CICLOS ECONÓMICOS DE GOODWIN
Goodwin (1967) propone una formalización de la dinámica del Ejército Industrial de Reserva, la cual se logra por medio de la combinación entre una curva de Phillips (la cual sirve para reflejar el balance de poder entre capitalistas y trabajadores) (Tarassow, 2010, p.4), la dependencia de la tasa de ahorro en la participación de los trabajadores en el producto, y la dinámica propia del empleo implícita en el modelo de Harrod (Shaikh, 2003, p.15).
Se asume una economía cerrada sin actividad del Gobierno, la producción puede usarse para el consumo o la inversión. Se asume la ley de Say y además todo el ahorro se destina a inversión (de hecho todas las ganancias se reinvierten). La productividad de la fuerza de trabajo se define aquí como el total de producto Y dividido para el total de fuerza de trabajo empleada L:
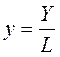 (1)
La tasa de empleo se define como la división entre la fuerza de trabajo empleada L y el total de fuerza de trabajo disponible η:
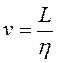   (2)
Se asume que existe una relación entre las variaciones en el salario real w y las variaciones de la tasa de empleo de la forma:
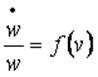   (3)
La participación de los trabajadores en el producto total se define como la división entre el total pagado a la fuerza de trabajo empleada dividido para el producto total:
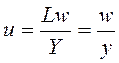   (4)
De (4) puede obtenerse la tasa de crecimiento aproximada de la participación de los trabajadores en el producto:

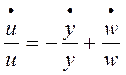
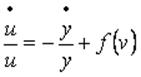 (5)
Luego, definiendo al plusproducto como la resta entre la producción y el total de salarios pagados a los trabajadores:
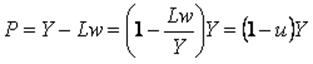  (6)
Y asumiendo que todo el plusproducto se destina al aumento del capital:
   (7)
Se puede obtener la tasa de crecimiento del capital en relación a la tasa de participación de los trabajadores en el producto:
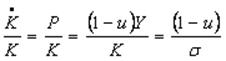  (8)
  
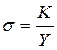
La relación entre producto neto y capital se denomina el “coeficiente de capital” que posee gran importancia en el modelo de Harrod-Domar. Definiendo además la relación entre capital y trabajo al estilo neoclásico3 :
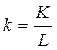 (9)
Expresándola en tasas de crecimiento:
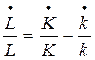    (10)
Luego, tomando la tasa de empleo y expresándola en tasa de cambio:
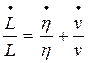  (11)
Igualando (10) y (11) e insertando estas en (8) se obtiene:


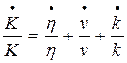
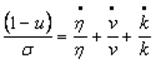
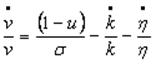(12)
De la expresión (5) y de la expresión (12) se obtiene un sistema de ecuaciones diferenciales:
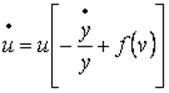 (13)
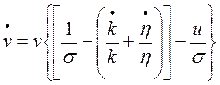 (14)
Estas ecuaciones diferenciales permiten describir la relación entre la tasa de empleo y la tasa de participación de los trabajadores en el producto por medio del comportamiento cíclico que poseen las funciones respuesta de este sistema de ecuaciones diferenciales.
Igualando a cero las expresiones (13) y (14) se obtienen valores “de equilibrio” de la tasa de empleo y la tasa de participación de los trabajadores (Weber, 2005, p. 9) 4:
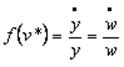   (15)
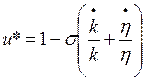    (16)
Si se asume una relación salario real-tasa de empleo de tipo lineal:
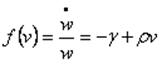  (17)
Se puede obtener el siguiente punto de “equilibrio” para la expresión 15:
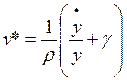 (18)
Entonces, con las expresiones (16) y (18) puede describirse las fluctuaciones de la economía de la siguiente manera: si la tasa de empleo es menor a su valor “de equilibrio” entonces la tasa de participación de los trabajadores en el producto empieza a disminuir, pero la disminución de la tasa de participación por debajo de su valor “de equilibrio” a su vez hace que el nivel de empleo empiece a recuperarse, sin embargo el sistema no llega a alcanzar un equilibrio en donde tanto la participación de los trabajadores como la tasa de empleo dejen de crecer. Más bien el sistema se mantiene en una oscilación “perfecta” alrededor de los puntos de “equilibrio” (Shaikh, 2003, p.17).
Fluctuación de la tasa de empleo y la participación de los trabajadores en el producto alrededor del “equilibrio”
La dinámica de este modelo corresponde al modelo de presa-depredador (caso particular de las ecuaciones de Lotka-Volterra) en donde la presa tiende a crecer indefinidamente a menos que exista un depredador que detenga su crecimiento, mientras que el depredador tiende a desaparecer a menos que “interactué” con la presa. Para este caso, Solow señalaría que en el modelo de Goodwin los obreros son los depredadores y las presas son los capitalistas o que los depredadores son los trabajadores con empleo y las presas los trabajadores sin empleo (1990).
BREVE EXTENSIÓN, EL PAPEL DE LA EXPLOTACIÓN SOBRE EL EMPLEO
El modelo arriba descrito no representa un camino “único” a la explicación de la lógica del comportamiento del empleo. De hecho hay que tomar en consideración que la tasa de participación de los trabajadores en el producto no es lo único que se afecta con las variaciones del empleo, pues existen muchos otros aspectos que poseen una relación importante con el empleo como son el plusvalor apropiado, el nivel de acumulación, la tasa de ganancia, la tasa de explotación, etc.
En este texto nos limitaremos a presentar la extensión más sencilla,  que vincula a la tasa de empleo y la tasa de explotación. Para realizar esto habrá que buscar la forma de reemplazar la tasa de participación de los trabajadores en el producto por la tasa de explotación dentro de la formulación original de Goodwin.
Retomando la definición de la tasa de participación de los trabajadores en el producto:
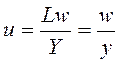   (4)
Y recordando la definición de la tasa de explotación:
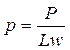    (19)
Se puede elaborar una relación algebraica entre ambas tasas. Si se recuerda que el producto neto se distribuye entre salarios y plusvalor:
    (20)
Entonces se puede reescribir (4) como:
  
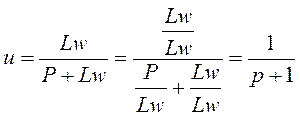
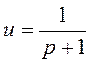 (21)
La tasa de participación de los trabajadores en el producto lleva en su interior a la tasa de explotación. Si hacemos un pequeño artificio para facilitar el cálculo:
  (22)
Notando que la expresión (22) sigue midiendo la explotación ya que lo único que se hizo es una “traslación dl origen” de cero a uno, entonces podemos decir que:
 
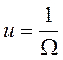
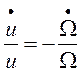  (23)
El crecimiento en la participación de los trabajadores en el producto provoca una disminución de la explotación. Si se reemplaza (23) en el sistema de ecuaciones (13-14) y se asume la curva de Phillips de la expresión (17) se obtiene el sistema:
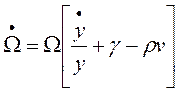 (24)
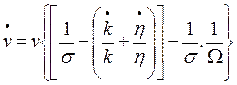 (25)
El cual difiere de la formulación original del modelo presa-depredador de Goodwin por lo cual hay la necesidad de comprender la lógica que siguen las respuestas de este sistema de ecuaciones pues existe la posibilidad de que las soluciones de este sistema ya no formen órbitas cerradas alrededor de “puntos de equilibrio”. Aplicaremos el mismo procedimiento de Goodwin (1967) a fin de obtener las funciones que definen la forma de las funciones solución del sistema (24-25)5 .
Representando a las expresiones (24) y (25) de una forma más simple:
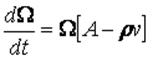 (26)
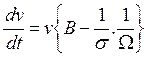 (27)
Se puede obtener las funciones solución de este sistema de ecuaciones diferenciales por medio de una igualdad que elimine a la “variación” del tiempo:
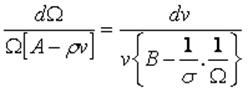 (28)
Reacomodando términos:


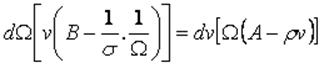
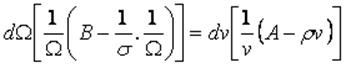
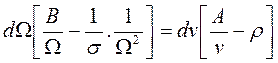 (29)
La expresión (29) puede resolverse por medio de una integración a ambos lados de la expresión:

 

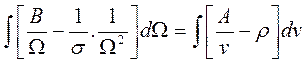
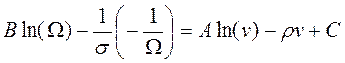
Donde C es una constante combinada de integración. Reemplazando los valores de A y B finalmente se obtiene:
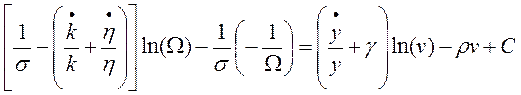 (30)
Que representa a las soluciones del sistema de ecuaciones (24-25), las cuales forman órbitas cerradas en torno a puntos de equilibrio.  
REPRESENTACIÓN GRAFICA
Para realizar una representación gráfica de la expresión (30) vamos a suponer las siguientes condiciones:
Se asume una economía cuyo stock de capital es de 10 unidades y su producción neta es de 5 unidades, es decir existe una relación capital-producto de 2. La tasa de crecimiento del capital por persona ocupada es del 10%. La tasa de crecimiento de la población económicamente activa es del 5%. La tasa de crecimiento de la productividad de la fuerza de trabajo es del 15%.
Estos datos en términos de la notación utilizada se describen como:
                 
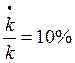
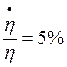
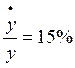
Además se asume la existencia de una curva de Phillips con la forma:

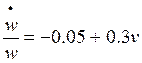
Con estos supuestos la relación entre tasa de explotación y tasa de empleo es:

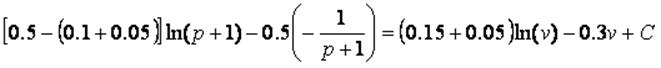
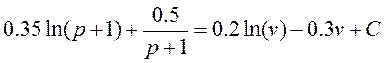 (31)
Dependiendo de las condiciones iniciales en que se encuentre la tasa de empleo y la tasa de explotación se pueden obtener los valores de C. Para cada valor de C, la solución (31) forma una órbita distinta alrededor de los valores de “equilibrio” de la tasa de empleo y de la tasa de explotación (a medida que C aumenta, la órbita se vuelve más amplia).
Soluciones distintas soluciones al sistema de ecuaciones diferenciales para distintas condiciones iniciales

En este caso los puntos de “equilibrio” pueden obtenerse igualando a cero las ecuaciones (24-25):
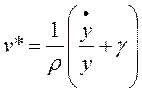  (32)
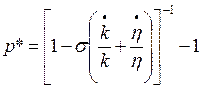 (33)
Que para los valores supuestos resultan ser:
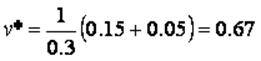  (34)
 (35)
Si además se supone que inicialmente la tasa de empleo es del 70% y que la tasa de explotación es del 100%, se puede obtener el valor de la constante C que en este caso resulta ser aproximadamente de 0.774.
Entonces la tasa de plusvalor y la tasa de empleo en la economía que posee los supuestos señalados se vinculan por medio de la relación 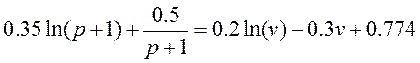(36):
 (36)
COMPORTAMIENTO CÍCLICO
Luego de determinar la relación (36), es importante conocer el sentido del comportamiento cíclico de la economía, es decir, dada la situación inicial, se desea saber qué sucederá con la tasa de explotación y la tasa de empleo con el paso del tiempo, asumiendo todo lo demás constante.6 En la situación inicial supuesta en el ejemplo numérico, la tasa de plusvalor es mayor a su valor “de equilibrio”, lo que igualmente sucede con la tasa de empleo, indicándonos que estamos en la región cuatro del gráfico siguiente:
Distintas regiones según los valores mayores e inferiores a los puntos “de equilibrio”
Por un lado, el efecto que produce una tasa de empleo mayor a su valor de equilibrio puede deducirse de la siguiente manera:
            
 
 
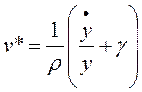
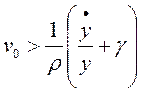
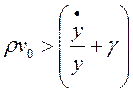
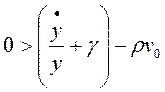 (37)
De (37) se concluye que una tasa de empleo mayor al “equilibrio” presiona a una disminución de la tasa de explotación (lo que se debe a que un aumento del empleo implica un aumento del salario a causa de la curva de Phillips utilizada como supuesto), comportamiento representado por la expresión 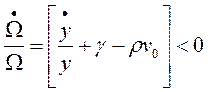(38):

  (38)
Por el otro lado, el efecto que produce una tasa de explotación mayor a su valor de equilibrio puede deducirse así:
         
  



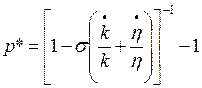
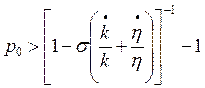
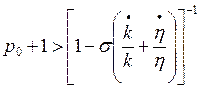
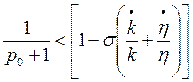
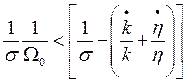
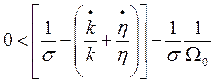 (39)
De (39) se concluye que una tasa de explotación mayor a su tasa “de equilibrio” presiona a un aumento de la tasa de empleo (lo que se justifica en que una tasa de explotación alta incentiva a los capitalistas a contratar más personas por la posibilidad de aumentar la masa de plusvalor a obtener, efecto que sin embargo de a poco va disminuyendo su intensidad debido a que se asumió que con el aumento del empleo se da un aumento de los salarios). Este comportamiento se representa por la expresión 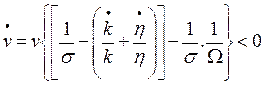(40):
 (40)
Con (39) y (40) se comprueba que los movimientos cíclicos de la economía en torno a sus valores “de equilibrio” en esta breve extensión siguen el mismo movimiento que el realizado por la economía en el modelo de Goodwin (es decir, en el sentido de las agujas del reloj).
Así, dada una tasa de explotación del 100% y una tasa de empleo del 70% y asumiendo todo lo demás constante, se esperará que a causa de la tasa de explotación mayor a su valor de equilibrio, los capitalistas tengan expectativas de aumentar la masa de plusvalor a obtener por medio de la contratación de más personas, lo cual provoca que la tasa de empleo suba, pero a su vez este hecho lleva a que los trabajadores adquieran mayor capacidad de presión para alcanzar aumentos de sus salarios (supuesto acorde a la lógica de la curva de Phillips utilizada como supuesto) lo que va disminuyendo la tasa de explotación hasta un punto tal que los capitalistas deciden dejar de contratar personas, haciendo que el empleo se estanque y luego empiece a contraerse.

Sentido de las fluctuaciones de la economía en torno a sus valores “de equilibrio”
Para visualizar la lógica en conjunto, se representan a continuación el sistema de ecuaciones (24-25) en términos de los valores numéricos utilizados en el ejemplo:
 
 
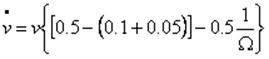
Es decir:
 (41)
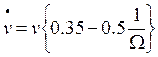 (42)
Este sistema de ecuaciones ya no representa un caso de presa-depredador como en el modelo de Goodwin, sino que este modelo es similar a un modelo de ecuaciones Lotka-Volterra para un caso competitivo, en donde por un lado la explotación puede crecer “sin límites” a menos que el empleo crezca y presione a un aumento de los salarios, mientras que el empleo también podría crecer “sin límites”, pero su mayor participación en el producto (equivalente a 1/Ω) disminuye la masa de plusvalor apropiada por los capitalistas, lo cual hace que estos cada vez decidan contratar menos personas hasta un punto en donde simplemente se deja de contratar y más bien se empieza a despedir gente.

CONCLUSIONES
Esta breve extensión del modelo de Goodwin permite visualizar el comportamiento del empleo en el capitalismo como parte del enfrentamiento de clases sociales antagónicas (trabajadores y burgueses) que no pueden cumplir sus objetivos con total plenitud dentro de la sociedad a causa de que no actúan solos, sino que están estrechamente interrelacionados. Así, la explotación en este modelo podría crecer “sin límites” si los trabajadores no logran presionar por un alza de salarios, mientras que la tasa de empleo podría crecer “sin límites” (en realidad tiene como máximo el 100%) si los trabajadores no encontraran obstáculos en la contratación por parte de los capitalistas.
Mientras que los capitalistas buscan explotar lo máximo la posibilidad de obtener plusvalor, por otro lado los trabajadores presionan por aumentar los salarios con miras a mejorar su situación de vida. La extensión aquí planteada permite “formalizar” los aspectos más generales de esta pugna sin realizar ningún cambio al modelo de Goodwin, sino simplemente realizando una reinterpretación de este modelo desde la tasa de explotación (que está directamente relacionada con la tasa de participación de los trabajadores en el producto utilizada por Goodwin).
Una ventaja del modelo de Goodwin (y de esta extensión que no ha agregado algo nuevo, sino solo mirar desde otro ángulo el problema de las fluctuaciones en el empleo cambiando el modelo presa-depredador por un modelo de competencia) es que no define la situación de una economía como un punto de equilibrio (de hecho a causa de las formas que tienen las funciones, el equilibrio en este modelo en la práctica jamás es alcanzable) sino como una continua fluctuación (que en nuestra extensión está claramente determinada por la lucha de clases) en torno hacia una tendencia que se determinar en términos muy generales.
Una desventaja del modelo de Goodwin (y a su vez de esta extensión) es que se mantiene la idea de que los aumentos de la productividad de la fuerza de trabajo provocan un incremento en el empleo “de equilibrio” (lo que puede verse, por ejemplo, en la expresión (32) en donde la tasa de empleo “de equilibrio” crece si crece la productividad de la fuerza de trabajo, pues están directamente relacionadas), lo cual está estrechamente ligado al planteamiento neoclásico y que se opone a la lógica de la ley general de la acumulación capitalista planteada por Marx (El Capital, Tomo I, Capítulo XXIII) en donde la lógica del Ejército Industrial de Reserva depende enormemente del proceso de reproducción ampliada del capital, pues es a causa de este proceso que nace y se desarrolla el Ejército Industrial de Reserva.
NOTA FINAL
Hay que recordar que ningún modelo matemático puede deducir el resultado de la lucha de clases entre trabajadores y burgueses y su efecto sobre el ciclo económico, lo único que se puede hacer es señalar las tendencias más generales (influenciadas por circunstancias diversas que en este caso por simplicidad se asumen como fijas) en torno a las cuales las dos clases sociales van pugnando, pero a la final el resultado concreto de esa pugna solo dependerá de la situación concreta que se analice.

REFERENCIAS
GOODWIN, R.M. (1967): “A Growth Cycle”, publicado en C. H. Feinstein, ed. Socialism, Capitalism and Economic Growth. Essays presented to Maurice Dobb. Cambridge: Cambridge UniversityPress, pp. 54-58.
SHAIKH, Anwar (2003): “Labor Market Dynamics within Rival Macroeconomic Frameworks”, publicado en: ARGYROUS, et al. (2003): “Growth, Distribution and Effective Demand: Alternatives to Economic Orthodoxy”, M.E. Sharpe, Armonk, NY: Capítulo 8, pp. 127-143. Ver: http://homepage.newschool.edu/~AShaikh/lmdynamics.pdf
SHAIKH, Anwar (2008): “Nonlinear Dynamics and Pseudo-Production Functions”, Eastern Economic Journal, Vol. 31, No. 3, 2005. Disponible en: http://homepage.newschool.edu/~AShaikh/Nonlinear%20Dynamics%20and%20Pseudo-Production%20Functions.pdf
SOLOW, Robert (1956). "A Contribution to the Theory of Economic Growth". Quarterly Journal of Economics (The MIT Press) 70: 65–94.
SOLOW, Robert (1990): “Goodwin's Growth Cycle: Reminiscence and Rumination”, publicado en Velupillai, J. (ed.) (1990): Nonlinear Multisectoral Macrodynamics, Londres, McMillan, pgs. 31-41.
TARASSOW, Artur (2010): “The empirical relevance of Goodwin’s business cycle model for the US economy”, MPRA, abril, 2010. Disponible en: http://mpra.ub.uni-muenchen.de/21815/
THE NEW SCHOOL FOR SOCIAL RESEARCH, New York, The History of economic thought website:  http://homepage.newschool.edu/~het/essays/multacc/goodw2.htm
WEBER, Lars (2005): “A Contribution to Goodwin’s Growth Cycle Model from a System Dynamics Perspective”, presentado en la 23ra conferencia de la Sociedad de Sistemas Dinámicos, Boston, julio, 2005. Disponible en: http://www.systemdynamics.org/conferences/2005/proceed/papers/WEBER196.pdf
REFERENCIA PARA LA GRÁFICA DE FUNCIONES IMPLÍCITAS
http://www.batesville.k12.in.us/physics/CalcNet/grapher/if_grapher.htm