ANÃLOGOS PERIÃDICOS DEL POLINOMIO DE INTERPOLACIÃN DE HERMITE
Gerardo Soler Leyva (CV)
soler@cug.co.cu
Universidad de GuantÃĄnamo
Resumen
En el artículo de T.N. Radchenko y V.S. Rogozhin [6], se utiliza un esquema sintético de solución del caso excepcional del problema de contorno de Riemann para las funciones analíticas, donde al transformar la condición de contorno original, interviene el polinomio de interpolación de Hermite. Es por eso que una de las cuestiones fundamentales en el estudio del caso excepcional del problema de contorno de Riemann para diferentes clases funcionales, lo constituye la construcción de análogos del polinomio de interpolación de Hermite que pertenezcan a las clases funcionales a las que pertenecerán las soluciones del problema que se estudia.
Nuestro objetivo con este trabajo es construir análogos del polinomio de interpolación de Hermite en las clases de funciones analíticas periódicas y biperiódicas.
Palabras clave: Función periódica, función periódica fundamental, paralelogramo de los períodos, función biperiódica, polinomio de interpolación de Hermite, análogo analítico periódico, análogo analítico biperiódico.
Abstract: T.N. Radchenko and V.S. Rogozhin [6] use a synthetic outline to solve the exceptional case of the Riemann boundary problem for the analytic functions, where when transforming the condition of original contour, takes part in the interpolation polynomial of Hermite. In this sense, one of the fundamental questions in the study of the exceptional case of the Riemann boundary problem for different functional classes, is the construction of similar of the interpolation polynomial of Hermite that belong to the functional classes to which will belong the solutions of the problem that are studied.
Our goal is to build some similar of interpolation polynomial of Hermite in the classes of analytic periodical and biperiodical functions.
Keywords: Periodical function, fundamental periodical function, paralelogram of periods, biperiodical function, Hermite interpolation polinomyal, periodical analytic analog, biperiodical analytic analog.
Introducción
Los problemas de contorno y en particular, el de Riemann, poseen importantes aplicaciones por ejemplo, en la resolución de ecuaciones integrales singulares [3, pág. 560], la Teoría de Aproximación de Funciones [3, pág. 634], la Teoría de las Colas [3, pág. 641], etc.
El problema de Riemann consiste en hallar una función F(z) analítica a trozos (F+(z) analítica en el dominio D+ y F-(z) analítica en el dominio D-) que satisfaga sobre el contorno suave cerrado L la condición
F+(t ) = G(t)F-(t) + g(t),
donde G(t) y g(t) satisfacen la condición de Holder y G(t) ¹ 0 sobre L, el cual divide al plano en el dominio interior D+ y el exterior D-. La condición de Holder significa que
½G(t2) – G(t1)½ < A½t2 – t1½l y ½g(t2) – g(t1)½ < B½t2 – t1½r
para dos puntos cualesquiera t1 y t2 de L, A>0, 0 < l ≤ 1 y 0 < r ≤ 1.
No es difícil darse cuenta de que si l > 1 y r > 1, las derivadas de las funciones se anulan, por lo que las funciones serán constantes.
Si se renuncia a las restricciones anteriores, o sea, si se admite que G(t) se anule en ciertos puntos de L o sea infinitamente grande de órdenes enteros, se obtiene el caso excepcional del problema de contorno de Riemann
F+(t ) = G(t)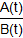 F-(t) + g(t),
F-(t) + g(t),
Donde 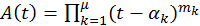 ,
, 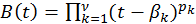 ,
, 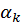 y
y 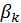 son puntos de L,
son puntos de L, 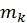 y
y 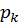 son enteros positivos.
son enteros positivos.
Actualmente se tiene la solución completa del problema de Riemann y también de diferentes generalizaciones. Una exposición de estos resultados se da en el libro de F.D. Gájov [3].
En el artículo de T.N. Radchenko y V.S. Rogozhin [6], se utiliza un esquema sintético de solución del caso excepcional del problema de contorno de Riemann con el empleo del polinomio de interpolación de Hermite.
La resolución de ecuaciones integrales, en general exige de ciertos procesos de aproximaciones sucesivas. Sin embargo, existen algunos tipos de ecuaciones integrales, para las cuales se puede obtener la solución en forma cerrada mediante la introducción de funciones auxiliares y el problema de contorno de Riemann. En el caso de ecuaciones integrales singulares con núcleo automorfo, la función buscada será automorfa.
La Teoría de Funciones Analíticas Automorfas, cuyas bases fueron elaboradas en los trabajos de F. Klein y A. Poincaré, representa una parte amplia de la Matemática. Estas funciones están estrechamente relacionadas con la Teoría de Ecuaciones Diferenciales, Teoría de las Superficies de Riemann, Topología, Geometría no Euclidiana y una serie de otros apartados de la Matemática. Una exposición de los resultados de esta teoría la da el libro de L. Ford [2].
De las investigaciones sobre funciones automorfas, es necesario destacar los trabajos de L. I. Chibríkova (ver, por ejemplo, [1]), relacionados con la solución del problema de contorno de Riemann en esa clase de funciones.
Por lo anterior, es de interés resolver el problema de contorno de Riemann en la clase de funciones automorfas, siendo una de las cuestiones fundamentales en el estudio del caso excepcional, la construcción de análogos del polinomio de interpolación de Hermite que pertenezca a la clase funcional a la que pertenecerá la solución del problema. En este sentido, nos proponemos mostrar un procedimiento para construir análogos del polinomio de interpolación de Hermite en las clases de funciones analíticas periódicas y biperiódicas.
Funciones automorfas.
El concepto de función automorfa constituye una generalización del concepto de función periódica. Consideremos el conjunto numerable de funciones lineales fraccionales
wk(z) = 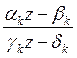 , Dk =
, Dk =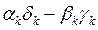 ¹ 0,
¹ 0,
k = 1, 2, …; w1(z) º z,
las cuales constituyen un grupo. Este grupo, en general, es infinito.
El punto z es llamado punto límite del grupo si es el límite de la sucesión wk(z) para algún z. Si z no es límite, entonces es llamado punto ordinario del grupo. Asimismo, el grupo es denominado discontinuo sobre el conjunto E, si es discontinuo en cada punto de este conjunto.
Los puntos o figuras que se obtienen uno del otro mediante las transformaciones del grupo se denominan congruentes. Un dominio que no contiene dos puntos distintos congruentes entre sí, recibe el nombre de dominio fundamental del grupo (este dominio a menudo es denominado polígono fundamental del grupo, donde se añaden puntos de la frontera, a saber, uno de dos lados congruentes y un vértice del conjunto de vértices congruentes).
Una clase importante de grupos, objeto de nuestra atención, está constituida por los grupos con un solo punto límite, entre los que se encuentran el periódico
wk(z) = z + kW, kÎZ, W≠0
y el biperiódico
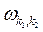 (z) = z + k1W1 + k2W2, k1, k2ÎZ, W1/W2 =
(z) = z + k1W1 + k2W2, k1, k2ÎZ, W1/W2 = 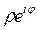 , j ≠ 2np.
, j ≠ 2np.
Los números W, W1 y W2 son llamados períodos fundamentales del grupo correspondiente.
Para el grupo periódico, su dominio fundamental será cualquier franja comprendida entre dos rectas, relacionada con la transformación w(z) = z + W, mientras que para el grupo biperiódico el domino fundamental será cualquier paralelogramo con lados paralelos de longitudes W1 y W2 respectivamente.
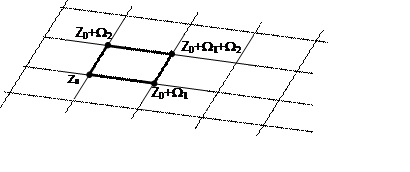
Fig. 1
La función analítica F(z) se denomina automorfa, perteneciente al grupo considerado, si ella es invariante respecto a las transformaciones de este grupo, es decir, si
F[wk(z)] = F(z), k = 1, 2, …
De la definición anterior se deduce que una función automorfa adquiere en los puntos congruentes los mismos valores. En este sentido, si F(z) posee en cierto punto z0 un cero o un polo, entonces en todos los puntos congruentes wk(z0) ¹ z0 ella también tendrá ceros o polos del mismo orden.
Las funciones automorfas se definen sólo para los grupos discontinuos. Sus dominios de existencia son dominios de discontinuidad para los grupos y están formados por los puntos ordinarios. Los puntos límite del grupo son puntos singulares para la función automorfa.
Como las funciones automorfas toman los mismos valores en los puntos congruentes, es suficiente considerarlas en el dominio fundamental del grupo.
Los puntos frontera de cualquier dominio fundamental forman un conjunto de lados (arcos) congruentes dos a dos. Para los grupos cuyo dominio fundamental tiene un número finito de lados, las funciones automorfas se denominan simples. Estas poseen propiedades notables como:
- Toda función automorfa simple F(z) diferente de una constante, posee en su dominio fundamental polos. El número de ceros y polos es el mismo y se llama orden de la función F(z) (los polos y ceros se consideran cada vez, teniendo en cuenta sus multiplicidades).
- Para cualesquiera dos funciones automorfas simples F1(z) y F2(z) de un grupo dado, existe un polinomio Q(u, v) de dos variables con coeficientes constantes, tal que
Q[F1(z), F2(z)] = 0.
- Si existe una función automorfa simple f(z) de un grupo dado, la cual posee un solo polo simple en el dominio fundamental, siendo analítica en los restantes puntos, entonces cada función automorfa simple del grupo es una función racional de f(z). Esta función es llamada función fundamental del grupo (o invariante fundamental del grupo).
Ejemplo 1. Todas las funciones automorfas simples, en el caso del grupo biperiódico, son funciones racionales de la función de Weierstrass
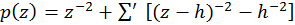 , h = k1W1 + k2W2
, h = k1W1 + k2W2
y su derivada p’(z):
F(z) = a1[p(z)] + a2[p’(z)].
El apóstrofe en el signo de suma significa que la misma se efectúa para todos los períodos h diferentes de cero.
Funciones periódicas.
Sea el grupo periódico
Sk(z) = z + kW, kÎZ, W>0
con período fundamental W, la cual contiene al origen de coordenadas. En este caso, una función automorfa recibe el nombre de función periódica de período W y el dominio fundamental del grupo, franja del período.
Ejemplo 2. En calidad de función periódica fundamental podemos tomar la función
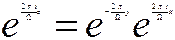 ,
,
la cual posee período W, se reduce a cero en el extremo superior de la franja del período y posee un polo simple en el extremo inferior. En este caso, la imagen de la franja del período del grupo Sk(z ) es todo el plano z, en el cual z = 0 y z = ¥ son los valores límites de la función 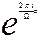 , cuando z permaneciendo en la franja del período, tiende respectivamente a sus extremos superior e inferior.
, cuando z permaneciendo en la franja del período, tiende respectivamente a sus extremos superior e inferior.
Efectivamente, bajo la aplicación 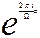 , el interior de la franja del período pasa a ser el plano z cortado a lo largo del semieje real positivo; las orillas del corte son las imágenes de las rectas que limitan a esta franja, pero al dominio fundamental se relaciona solamente una de estas rectas ya que los puntos de las mismas son congruentes respectivamente a la transformación S1(z) = z + W.
, el interior de la franja del período pasa a ser el plano z cortado a lo largo del semieje real positivo; las orillas del corte son las imágenes de las rectas que limitan a esta franja, pero al dominio fundamental se relaciona solamente una de estas rectas ya que los puntos de las mismas son congruentes respectivamente a la transformación S1(z) = z + W.
Funciones biperiódicas.
Sea el grupo biperiódico
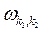 (z) = z + k1W1 + k2W2,
(z) = z + k1W1 + k2W2,
donde k1, k2 = 0, ±1,…, W1 y W2 son números complejos diferentes de cero tales que Im(W1/W2) ≠ 0.
A través de los períodos fundamentales del grupo cualquier período puede ser representado en la forma W = k1W1 + k2W2; donde k1 y k2 son ciertos números enteros positivos y/o negativos.
Sea R1 uno de los dominios fundamentales del grupo, constituido por todos los puntos interiores, los lados (z0, z0 + W1), (z0, z0 + W2), y el vértice z0 del paralelogramo con vértices
z0, z0 + W1, z0 + W1 + W2, z0 +W2,
donde z0 es un punto arbitrario (Fig. 1).
A R1 se le llama paralelogramo de los períodos y a las funciones automorfas simples pertenecientes al grupo, biperiódicas.
Consideraremos el recorrido de la frontera del paralelogramo de los periodos R1 positivo, si a él corresponde el orden de los vértices z0, z0 + W1, z0 + W1 + W2, z0 +W2.
Polinomio de interpolación de Hermite.
Es conocido (ver, por ejemplo [4]) el siguiente problema generalizado de interpolación, considerado por el matemático francés Charles Hermite (1822 – 1901): “Constrúyase un polinomio P(x) de grado n, tal que en s puntos diferentes 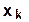 (k=1, 2,…,s) tome junto a sus derivadas de orden h (h=0,1,...,
(k=1, 2,…,s) tome junto a sus derivadas de orden h (h=0,1,..., 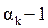 ) los valores dados
) los valores dados 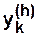 según las condiciones:
según las condiciones:
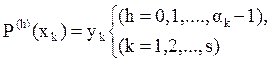
con la particularidad de 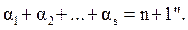
Los puntos xk son llamados nodos de interpolación y los números αk sus multiplicidades respectivamente.
El polinomio obtenido, denominado Fórmula de Hermite, tiene la forma:
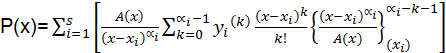 ,
,
donde 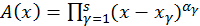 y
y 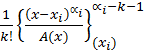 es la suma de los términos del desarrollo de la función
es la suma de los términos del desarrollo de la función 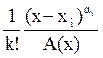 en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
Si 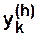 son los valores de las derivadas de cierta función f(x) en los puntos correspondientes, entonces se obtiene la siguiente fórmula de interpolación mucho más general:
son los valores de las derivadas de cierta función f(x) en los puntos correspondientes, entonces se obtiene la siguiente fórmula de interpolación mucho más general:
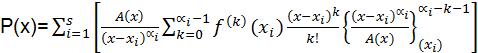 (1)
(1)
donde 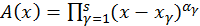 y
y 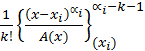 es la suma de los términos del desarrollo de la función
es la suma de los términos del desarrollo de la función 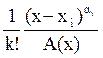 en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
Observación 1. Si las multiplicidades de los nodos αi son iguales a 1, es decir, si todos los nodos son simples, la fórmula (1) se convierte en la conocida fórmula de Lagrange
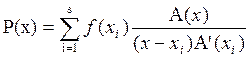 .
.
Observación 2. Si se tiene un solo nodo x=a de multiplicidad a, entonces 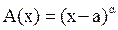 y en lugar de (1) se tendrá el tramo de la serie de Taylor del desarrollo de la función f(x) en la vecindad del punto a
y en lugar de (1) se tendrá el tramo de la serie de Taylor del desarrollo de la función f(x) en la vecindad del punto a
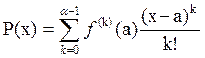 .
.
Ejemplo 3. Vamos a construir un polinomio P(x) de grado cinco que cumpla las condiciones, P(0) = 1, P’(0) = 0, P’’(0) = 2, P(1) = -1, P’(1) = 0 y P(2) = 0.
En este caso A(x) = x3(x-1)2(x-2). Luego
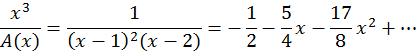
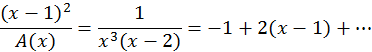
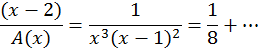
Podemos escribir entonces:
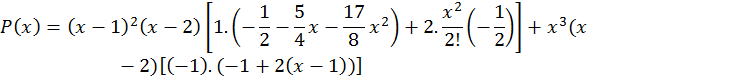
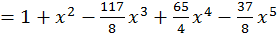 .
.
Análogos del polinomio de interpolación de Hermite.
Análogo analítico periódico.
Consideremos el polinomio de interpolación de Hermite Q(z) para la función analítica f(z), con nodos de interpolación αk de multiplicidades mk respectivamente según la fórmula (1) (k=1,2,…,μ). En este caso, se verifican las igualdades
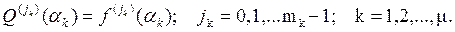
Sean 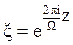 y
y 
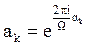 . Considerando lo señalado para las funciones periódicas y el polinomio de interpolación de Hermite, ya no representa ninguna dificultad percatarse del cumplimiento del siguiente teorema:
. Considerando lo señalado para las funciones periódicas y el polinomio de interpolación de Hermite, ya no representa ninguna dificultad percatarse del cumplimiento del siguiente teorema:
Teorema 1. La función Q(ξ) es periódica de período Ω y es el “polinomio de interpolación de Hermite” de la función f(z), con nodos de interpolación 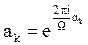 ; k=1,2,…,μ.
; k=1,2,…,μ.
Análogo analítico biperiódico.
Caso de un número finito de nodos simples. Aquí se exige construir una función 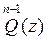 analítica biperiódica, que en n puntos dados
analítica biperiódica, que en n puntos dados 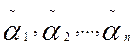 tome respectivamente los valores f1, f2,…,fn, es decir,
tome respectivamente los valores f1, f2,…,fn, es decir,
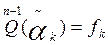 ; k=1,2,…,n. (2)
; k=1,2,…,n. (2)
El problema de encontrar la función biperiódica 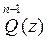 , podemos plantearlo en la siguiente forma: “se exige encontrar una función
, podemos plantearlo en la siguiente forma: “se exige encontrar una función 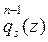 analítica biperiódica, que se reduzca a cero en los puntos
analítica biperiódica, que se reduzca a cero en los puntos 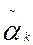 ; k=1,2,…,n, excepto en el punto
; k=1,2,…,n, excepto en el punto 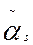 (
(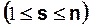 en el cual tome el valor 1” (ver [4], pág. 45).
en el cual tome el valor 1” (ver [4], pág. 45).
De esta forma, la función 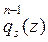 debe satisfacer las condiciones;
debe satisfacer las condiciones;
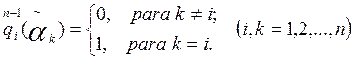
Si se logra construir 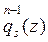 , entonces ya no representa trabajo construir la función
, entonces ya no representa trabajo construir la función 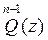 . En efecto, de (2) se deduce que la función
. En efecto, de (2) se deduce que la función 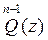 se determina mediante la fórmula
se determina mediante la fórmula
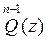 =
=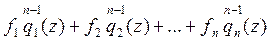 . (3)
. (3)
Por cuanto los ceros de la función biperiódica 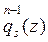 deben ser los números
deben ser los números 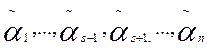 , ella puede tener la forma
, ella puede tener la forma
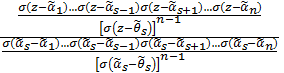 =
=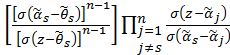
donde la función σ(u) se define ([5], pág. 179) por medio de la fórmula 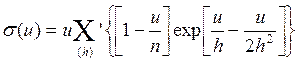 (σ-función de Weierstrass), en la cual el producto se efectúa para todos los períodos h = k1W1 + k2W2 diferentes de cero, lo que está señalado con un apóstrofe en el signo de multiplicación. Además,
(σ-función de Weierstrass), en la cual el producto se efectúa para todos los períodos h = k1W1 + k2W2 diferentes de cero, lo que está señalado con un apóstrofe en el signo de multiplicación. Además, 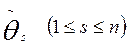 son puntos diferentes entre sí que satisfacen las correlaciones
son puntos diferentes entre sí que satisfacen las correlaciones
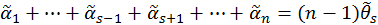 .
.
Sustituyendo las expresiones de 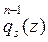 en (3), obtendremos
en (3), obtendremos
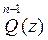 =
=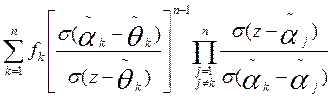 .
.
Sea 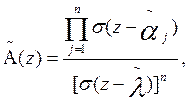 donde
donde 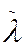 es un punto no coincidente con ninguno de los puntos
es un punto no coincidente con ninguno de los puntos 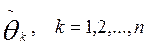 y que satisfacen la condición
y que satisfacen la condición 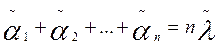 . De aquí se sigue que el factor
. De aquí se sigue que el factor 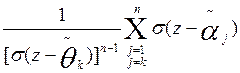 en la expresión (3) es igual a
en la expresión (3) es igual a 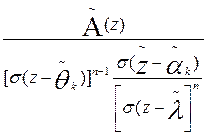 Por eso, se puede llevar (3) a una expresión, análoga a la fórmula de Lagrange, lo que se expresa mediante el teorema:
Por eso, se puede llevar (3) a una expresión, análoga a la fórmula de Lagrange, lo que se expresa mediante el teorema:
Teorema 2. La función
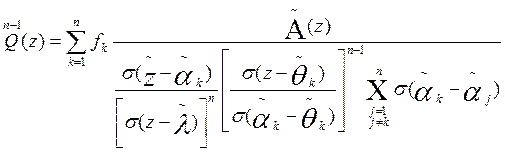
es bioperiódica y satisface las condiciones (2).
Observación 3. La función σ(u) es entera y posee ceros simples en los puntos u=h.
Observación 4. 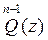 posee estructura de función biperiódica, sin embargo cuando, por ejemplo n=2, ella no es biperiódica, ya que tiene un polo simple y un cero simple y en el paralelogramo de los períodos R1, no puede existir ninguna función elíptica de primer orden ([1], pág. 210). Cada función automorfa simple, es decir, cada función cuyo dominio fundamental tiene un número finito de lados, posee polos en el mismo.
posee estructura de función biperiódica, sin embargo cuando, por ejemplo n=2, ella no es biperiódica, ya que tiene un polo simple y un cero simple y en el paralelogramo de los períodos R1, no puede existir ninguna función elíptica de primer orden ([1], pág. 210). Cada función automorfa simple, es decir, cada función cuyo dominio fundamental tiene un número finito de lados, posee polos en el mismo.
Caso de un nodo múltiple. En este caso, se exige hallar tal función Qn (z) analítica biperiódica, la cual en un punto dado 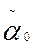 satisfaga las siguientes condiciones:
satisfaga las siguientes condiciones:
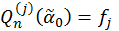 , j = 0, 1,…, n; (4)
, j = 0, 1,…, n; (4)
donde fj son valores dados.
La función Qn (z) debe tener la forma
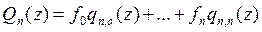 ,
,
donde
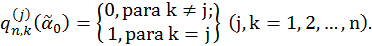
Vamos a demostrar por inducción que tal función se puede construir; al mismo tiempo indicaremos el modo de su construcción.
Si n=0, entonces la misma constante f0 sirve en calidad de función Q0 (z).
En el caso cuando n=1, tenemos 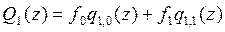 .
.
Tomemos 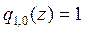 . De aquí tendremos que
. De aquí tendremos que 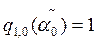 y
y 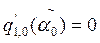 .
.
Sea 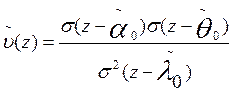 , donde los puntos
, donde los puntos 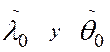 no coinciden entre si y
no coinciden entre si y 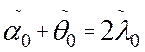 .
.
La función 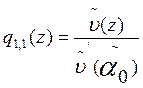 satisface las condiciones
satisface las condiciones 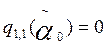 y
y 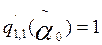 . Por eso,
. Por eso,
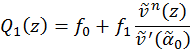
.
Supongamos que ya se ha hallado la función 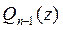 , la cual satisface las condiciones correspondientes. Es válido el siguiente teorema:
, la cual satisface las condiciones correspondientes. Es válido el siguiente teorema:
Teorema 3. La función
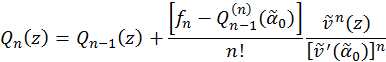
es bioperiódica y satisface las condiciones (4).
Demostración. Es suficiente demostrar que la función 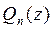 satisface las condiciones (4).
satisface las condiciones (4).
Por cuanto 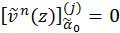 para j=0,1,…, n-1; tenemos que:
para j=0,1,…, n-1; tenemos que:
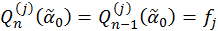 ; j=0,1,…,n-1. (5)
; j=0,1,…,n-1. (5)
Luego, hallemos la derivada de orden n de la función 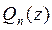 :
:
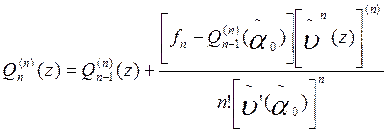 .
.
De ahí y considerando que 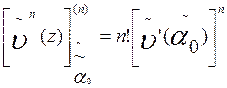 , obtendremos
, obtendremos
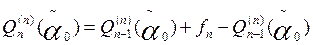 , es decir,
, es decir,
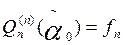 . (6)
. (6)
Uniendo (5) y (6) obtendremos las condiciones (4). El teorema queda demostrado.
Bibliografía
- Chibrikova L.I. (1977), Problemas de contorno fundamentales para las funciones analíticas. Kazán: Editorial Universidad de Kazán.
- Ford L. Funciones automorfas. –M. –L: ONTI.
- Gájov F.D. (1980), Problemas de contorno. Moscú: MIR.
- Goncharov V. L. (1954), Teoría de interpolación y aproximación de funciones. Moscú: Editorial Estatal de Literatura Teórica de Mecánica.
- Gurvits A., Courant R. (1968), Teoría de funciones. Moscú: Ciencia.
- Radchenko T. N, Rogozhin V. S. (1984), ¨Acerca de la Teoría del caso singular de la ecuación integral singular con núcleo de Cauchy y el problema de contorno de Riemann¨, Matemática (publicación de los Centros de Educación Superior de la URSS), N0 10: páginas 64-70.
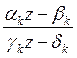 , Dk =
, Dk =
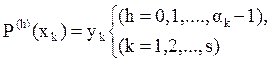
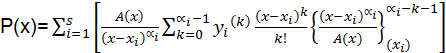 ,
,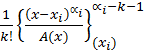 es la suma de los términos del desarrollo de la función
es la suma de los términos del desarrollo de la función 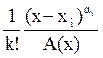 en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.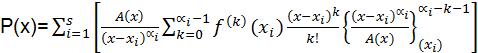 (1)
(1)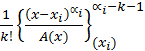 es la suma de los términos del desarrollo de la función
es la suma de los términos del desarrollo de la función 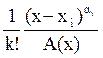 en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.
en serie de Taylor en una vecindad del punto xi, cuyas potencias no son mayores que αi-k-1.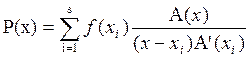 .
.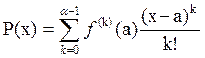 .
.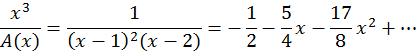
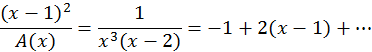
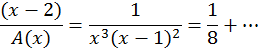
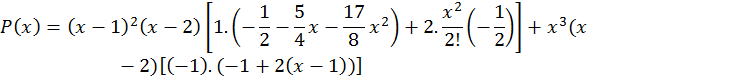
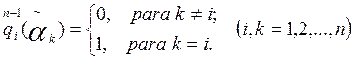
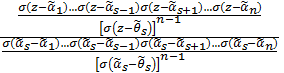 =
=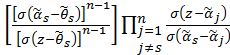
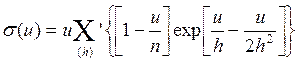 (σ-función de Weierstrass), en la cual el producto se efectúa para todos los períodos h = k1W1 + k2W2 diferentes de cero, lo que está señalado con un apóstrofe en el signo de multiplicación. Además,
(σ-función de Weierstrass), en la cual el producto se efectúa para todos los períodos h = k1W1 + k2W2 diferentes de cero, lo que está señalado con un apóstrofe en el signo de multiplicación. Además, 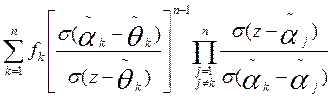 .
. 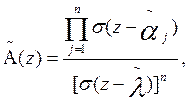 donde
donde 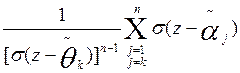 en la expresión (3) es igual a
en la expresión (3) es igual a 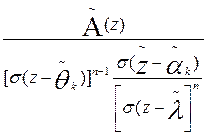 Por eso, se puede llevar (3) a una expresión, análoga a la fórmula de Lagrange, lo que se expresa mediante el teorema:
Por eso, se puede llevar (3) a una expresión, análoga a la fórmula de Lagrange, lo que se expresa mediante el teorema: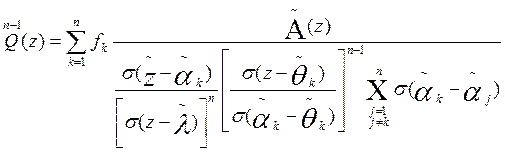
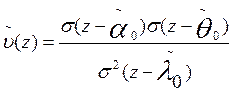 , donde los puntos
, donde los puntos 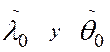 no coinciden entre si y
no coinciden entre si y 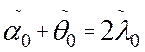 .
.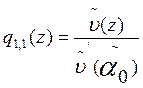 satisface las condiciones
satisface las condiciones 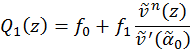
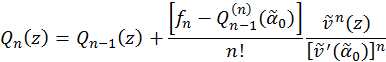
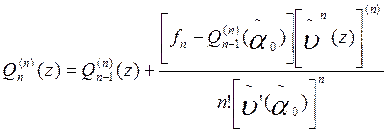 .
.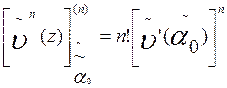 , obtendremos
, obtendremos 