Pulse aquí para acceder al índice general del libro. Pulse aquí para bajarse el libro completo en formato PDF comprimido ZIP, además de ejercicios prácticos en hojas XML, (92 páginas, 1512 Kb)

César Aching Guzmán

Valor Futuro de una anualidad

Al tratar el cálculo de las anualidades, determinábamos el valor de los flujos en valor actual o del momento cero. También es posible emplear esta misma formulación y plantear por ejemplo, cuánto tendré ahorrado en un momento futuro si depositara una determinada cantidad igual período a período, dada una cierta tasa de interés por período. Es decir, lo que estamos haciendo es constituir un fondo.

Anteriormente calculamos el valor actual de una serie de pagos futuros. Lo que ahora buscamos, como monto futuro, es una expresión que responda al siguiente perfil financiero:

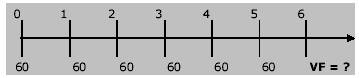
Partimos depositando una suma ahora y hacemos lo mismo con igual monto hasta el período n-1 y con la misma tasa de interés por cada período.

La fórmula del valor futuro de la anualidad y las derivadas de ella son: 

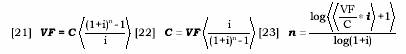
El valor, depende sólo de las variables tasa de interés «i», igual para cada período y el valor correspondiente al número de periodos «n», para flujos realizados a comienzo de cada uno de ellos.

Las anualidades tienen la característica que siendo un pago constante en el caso de amortizar una deuda los intereses pagados en los primeros periodos son mayores, destinándose el excedente al pago de amortización de capital, el cual aumenta gradualmente, el interés posterior deberá calcularse sobre un menor monto de capital por la disminución o amortización de éste.       

EJERCICIO 22 (Calculando el VF y el plazo de un ahorro)

Un microempresario deposita  UM 2,500 ahora en una cuenta de ahorros que reconoce una tasa de interés del 1.8% mensual  y  considera retirar UM 390 mensuales, empezando dentro de 10 meses. ¿Calcular por cuánto tiempo podrá  realizar retiros completos?

Solución:       

VA = 2,500;   i = 0.018;   C = 390;   n = 10;    VF = ?;   n = ?

1º Calculamos el VF de los UM 2,500 a 10 meses:

[11]  VF = 2,500(1 + 0.018)10 = UM  2,988.2559

2º Calculamos el tiempo durante el cual podrá hacer retiros por UM 390 cada uno:

Respuesta:

A partir del mes 10  puede  hacer  retiros completos por  7 meses.